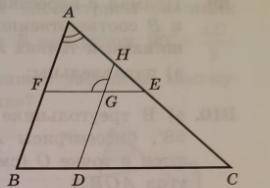
На сторонах AB и BC треугольника ABC выбраны точки F и D соответственно, а на стороне AC выбраны точки H и E так, что HD || AB, FE || BC. Найдите угол FGH если угол A = 68 угол C= 43
Другие вопросы по теме Геометрия
Популярные вопросы
- Выполните деление 3m^2-3n^2/m^2+mp: 6m-6n/p+m( вопрос так же есть на фото) ...
2 - What was the last movie you saw? How was it?...
2 - 7. Eceпте 825 г: 52 ц 10 кг : 23 ц: 26 мин 6 с: 3410 см: 54 см 3 мм: 24 м 59 см...
2 - Хппхпхпэпппэ I give 50 points ...
3 - Сообщение/конспект государственная политика в области торговли ДНР...
1 - Pозподіліть у три групи наведені речовини: водень, магній оксид. повітря, вода,...
2 - Дан угол Запишите его название и укажите а) вершину угла б) стороны угла...
1 - Complete the text with the words from the box....
3 - отрывок из сказки о животных используя полные или краткие прилагательные ( нужно...
3 - Менің Дағыстаным негізгі кейіпкер кім?...
2
Вспомним формулу площади треугольника через угол
S=0.5absina
Пусть BP=x , тогда AB=3x
Пусть BQ=4y , тогда BC=5y
\frac{S_{BPQ}}{S_{ABC}}=\frac{0.5*BP*BQ*sinaB}{0.5*AB*BC*sinB}=\frac{BP*BQ}{AB*BC}=\frac{4}{15}
S_{BQP}=\frac{4}{15}S_{ABC}
S_{APQC}=S_{ABC}-\frac{4}{15}S_{ABC}=\frac{11}{15}S_{ABC}
\frac{S_{ACPQ}}{S_{BPQ}}=\frac{11}{4}=2,75
ответ: 2,75
Объяснение: