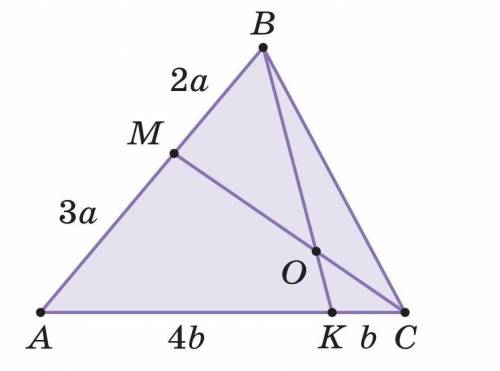
На сторонах  AB и  AC треугольника  ABC взяли точ- ки M и K так, что AM : BM = 3 : 2, AK : CK = 4 : 1.

Отрезки  BK и  CM пересекаются в  точке  O

Найдите  BO : OK.

Для решения этой задачи мы воспользуемся теоремой Менелая и подобием треугольников. 1. Из теоремы Менелая для треугольника ABC с учетом точек M и K на сторонах получаем: AM/MB * BK/KC * CO/OA = 1. Подставим известные значения: AM/MB = 3/2 и AK/CK = 4/1. Получаем (3/2) * BK/KC * CO/OA = 1. 2. Посмотрим на треугольники BAC и BKO. У них есть общий угол B и они подобны, так как угол BOA является вертикальным, а угол BKC - соответственным углом. Поэтому отношение длин отрезков BO и OA равно отношению длин отрезков BK и KC: BO/OA = BK/KC. 3. Аналогично, рассмотрим треугольники CAB и CMO. Они тоже имеют общий угол C и подобны. Следовательно, отношение длин отрезков CO и OA равно отношению длин отрезков CM и MA: CO/OA = CM/MA. 4. Из полученной ранее теоремы Менелая (3/2) * BK/KC * CO/OA = 1, заменим отношения BO/OA и CO/OA из пунктов 2 и 3, получаем: (3/2) * BK/KC * (CM/MA) = 1. Подставляем известные значения: MA/MB = 2/3 и CM/MA = 4/1. Получаем: (3/2) * BK/KC * (4/1) = 1. 5. Упростим последнее уравнение: (3/2) * BK/KC * 4/1 = 1, BK/KC = 2/3. 6. Если отношение длин отрезков BK и KC равно 2/3, то отношение длин отрезков BO и OK также равно 2/3. Итак, мы нашли, что BO : OK = 2 : 3.