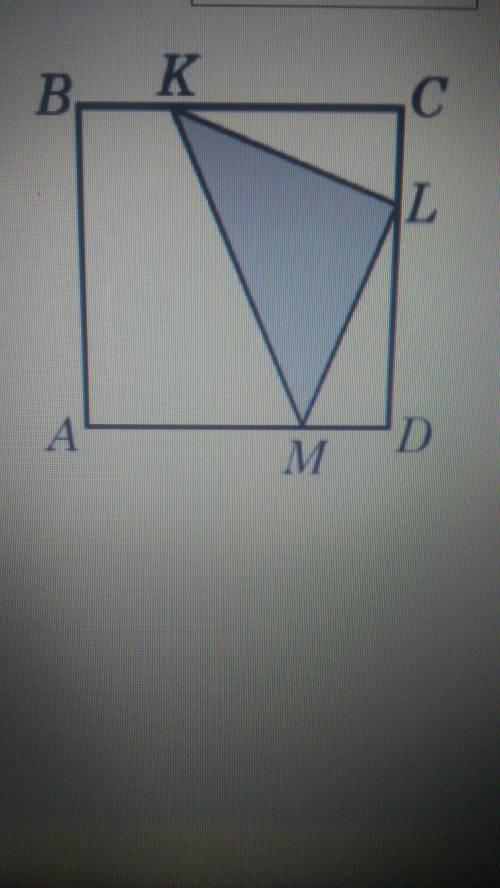
На рисунку зображено квадрат ABCD. Точки K, L, M належать сторонам ВС, CD та AD відповідно, BK=8 см. Трикутники KCL та LDM рівні, KC=LD=15 см. 1. Визначте довжину відрізка KL (у см). 2. Обчисліть площу трикутника KLM (у см2).
Другие вопросы по теме Геометрия
Популярные вопросы
- 1.Які дії Німеччини свідчили про її відмову від виконання положень Версального...
3 - Як визначити силу гравітаційної взаємодії двох куль у момент їх зіткнення, якщо...
2 - с во Какие мероприятия может осуществлять владелец фирмы для повышения эффективности...
3 - Найдите корень квадратного тричлена 2х²+11х+5...
2 - Що змусило Івана Дідуха емігрувати до Канади? Чи можна було знайти інший б вирішення...
2 - 8 клас Самостійна робота з теми «Основні класи неорганічних сполук. Оксиди, основи»1.Укажіть...
2 - До ть написати твір: опиши друга методом Шерлока Холмса...
2 - Выпишите из словарей 10 профессиональных слов, дайте их определение. Составьте...
1 - Знайти суму перших шести членів геометричної прогресії (bn) якщо b2=12,b4=-6...
2 - Укажіть рядок, у якому є помилка у написанні слів.А: воронезький, празький, брацький,...
3
ответ: KL=17см, S∆KLM=144,5см²
Объяснение: если ВК=8, а КС=15, то ВС=8+15=23см. Так как КС=LD, то CL=MD=BK=8см. Площадь квадрата - это квадрат его стороны: Sавсd=ВС²=23²=529см²
Теперь найдём площадь ∆КСL по формуле: S∆KCL=½×KC×CL=½×8×15=60см²
Таких треугольников 2, поэтому сумма их площадей=60×2=120см²
S∆KCL+S∆MLD=120см²
KM делит квадрат на 2 равные по площади части, поскольку ВК=DM, a KC=AM. Skcdm=529÷2=264,5см²
Теперь вычтем от площади KCDM площади 2-х треугольников и получим площадь ∆KLM:
S∆KLM=264,5-120=144,5=см²
KL- является гипотенузой в ∆KCL
Найдём гипотенузу KL по теореме Пифагора: KL²=KC²+CL²=15²+8²=225+64=
=289см
KL=√289=17см