На рисунку MN = NK , кутN=b МAперпендикулярноNK, NA=а. Знайти Р MNK і S MNK
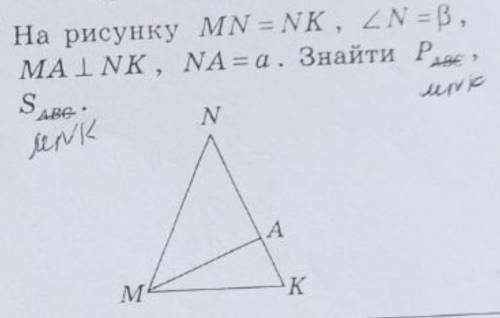
Другие вопросы по теме Геометрия
Популярные вопросы
- СОР СДЕЛАЙТЕ что ты можешь сказать о Кроне и Зевсе...
1 - Имя прилагательное в предложении может быть (найдите верное утверждение):...
1 - Спростіть вираз та знайдіть його значення (упростите выражение и найдите...
2 - Арман за первый час выполнил 2/3 часть дз , за 2 час на 1/7 меньше....
2 - Яку мову і чому використовували для написання книг...
1 - 1. Порівняйте маси золотої і срібної сережок, якщо об єм золотої в...
3 - Числа:h/d и d/h1/f и f/21/l и lЯвляются взаимно обратными? Заранее...
1 - 1. Дайте определение термину «трагедия» и назовите основные признаки...
2 - там два задания только быстро ...
2 - Летят два попугая один зелёный другой на север, сколько будет стоить...
3
Чтобы решить эту задачу, воспользуемся знаниями о прямоугольных треугольниках и площади треугольников.
1. Рассмотрим треугольник MNK.
У нас есть данные, что MN = NK, а кут N равен b градусов. Это говорит нам о том, что угол MKN является прямым, так как угол внутри равнобедренного треугольника (где две стороны равны) равен 90 градусам.
Теперь мы можем приступить к поиску периметра треугольника MNK.
Периметр треугольника вычисляется по формуле Р = AB + BC + AC.
Мы знаем, что MN = NK, значит, AB = NK. Из условия задачи также следует, что NA = а, а у нас есть прямой угол MKA. Значит, мы можем выразить длину AC через а и НK. AC = √(NA^2 + NK^2) = √(а^2 + NK^2).
Теперь мы можем записать формулу для вычисления периметра Р: Р = NK + NK + √(а^2 + NK^2) = 2NK + √(а^2 + NK^2).
2. Теперь рассмотрим площадь треугольника MNK.
Формула для вычисления площади треугольника, если известны две стороны треугольника и угол между ними, S = 0.5 * AB * BC * sin(N).
В нашем случае, AB = NK, BC = MN = NK (так как треугольник равнобедренный), и угол N равен b градусов.
Теперь мы можем записать формулу для вычисления площади S: S = 0.5 * NK * NK * sin(b) = 0.5 * NK^2 * sin(b).
Таким образом, мы получили формулы для вычисления периметра и площади треугольника MNK.
Для конкретного решения задачи, нам нужно знать значения а и b, чтобы мы могли подставить их в формулы и получить численные ответы.