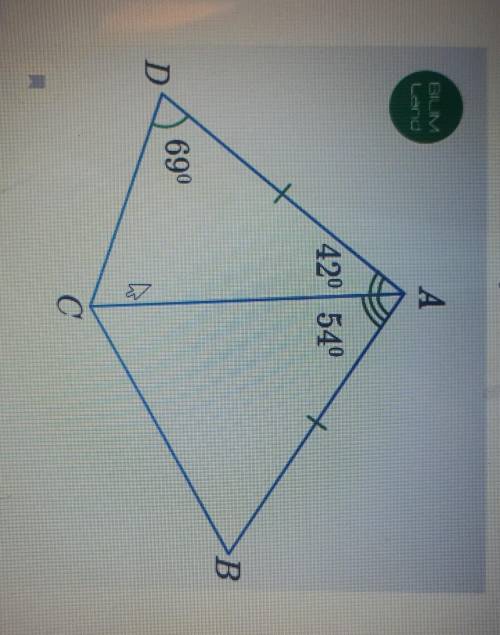
На рисунке в четырехугольнике ABCD, AD=AB. Найди угол ABC
​

Для решения данной задачи нам понадобятся знания о свойствах четырехугольников и свойствах равнобедренных треугольников.

Из условия задачи известно, что отрезок AD равен отрезку AB. Поэтому у нас имеется равнобедренный треугольник ABD, так как две его стороны (AD и AB) равны.

Из свойства равнобедренных треугольников мы знаем, что у него равны основания угла при вершине (у нас это угол B) и углы при основаниях (у нас это углы DAB и DBA). Поэтому угол DAB должен быть равным углу DBA.

Для решения задачи найдем значение угла DAB.

Мы знаем, что сумма углов в любом треугольнике равна 180 градусов.

Угол DAB + угол DBA + угол ADB = 180 градусов.

Угол DBA и угол ADB - это углы прямоугольного треугольника BDA. Так как уже известно, что угол DAB равен углу DBA, то обозначим его общей переменной "x".

Теперь мы можем записать уравнение:

x + x + 90 = 180.

Решим его:

2x + 90 = 180,
2x = 180 - 90,
2x = 90,
x = 45.

Таким образом, уголь ABC равен 45 градусам.