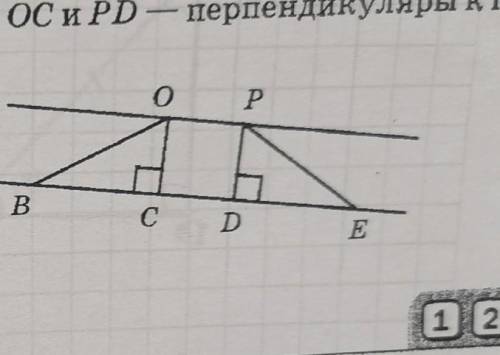
На рисунке прямые ОР и ВЕ параллельны, ОС и PD перпендикулярны к прямой ВЕ. Укажите верные утверждения;
1.ВС=DE
2.ОС=PD
3. Если угол OBC= Углу DEP,то треугольник ОВС=треугольнику РЕD

Добрый день!

На данном рисунке видно, что прямые ОР и ВЕ параллельны, а ОС и PD перпендикулярны к прямой ВЕ. Мы можем использовать эти данные, чтобы проверить верность каждого утверждения.

Утверждение 1: ВС=DE
Чтобы проверить это утверждение, нам нужно использовать свойство параллельных прямых, которое гласит, что если две параллельные прямые пересекают третью прямую (в данном случае ВЕ), то соответствующие отрезки на этих прямых равны. Итак, чтобы убедиться, что ВС=DE, нам нужно сравнить их длины.

На рисунке видно, что отрезки ВС и DE соединены перпендикулярами из точек C и D соответственно. Так как эти перпендикуляры параллельны, мы можем заключить, что отрезки ВС и DE равны. Поэтому первое утверждение верно: ВС=DE.

Утверждение 2: ОС=PD
Аналогично первому утверждению, мы можем использовать свойство перпендикуляров, которое гласит, что если перпендикуляры опущены из одной точки на параллельные прямые, то эти перпендикуляры равны. Итак, чтобы убедиться, что ОС=PD, нам нужно сравнить их длины.

На рисунке видно, что отрезки ОС и PD соединены перпендикулярами из точек C и D соответственно. Поскольку эти перпендикуляры равны, мы можем заключить, что отрезки ОС и PD равны. Поэтому второе утверждение верно: ОС=PD.

Утверждение 3: Если угол OBC= Углу DEP,то треугольник ОВС=треугольнику РЕD
Чтобы проверить это утверждение, мы должны сравнить треугольники ОВС и РЕD, основываясь на равенстве углов.

На рисунке видно, что углы OBC и DEP равны, так как они являются соответствующими углами при пересечении двух параллельных прямых (ОР и ВЕ) пересекаются с прямой (ОС и PD).

Однако, для полной проверки равенства треугольников требуется также равенство длин сторон. На рисунке видно, что длины отрезков ОС и PD равны, как мы уже установили в утверждении 2. Но для полной проверки, нам не хватает информации о длинах других сторон треугольников (ОВ, ВС и РЕ, DE).

Таким образом, мы можем утверждать только, что угол OBC= Углу DEP, но не можем с уверенностью сказать, что треугольник ОВС=треугольнику РЕD без дополнительных данных о длине сторон треугольников.

Вывод:
1. ВС=DE
2. ОС=PD
3. Мы можем утверждать только, что угол OBC= Углу DEP, но не можем с уверенностью сказать, что треугольник ОВС=треугольнику РЕD без дополнительных данных о длине сторон треугольников.