На рисунке OD=OB, CD=CB. Найдите ОB, если AD=10 см,
∠BAD=60
∘

. ответ

OB = 5 см.

Объяснение:

Треугольник ΔBAO = ΔDAO так как ∠BAO = ∠DAO и BO = AO по условию, то отрезок AO - является биссектрисой и медианой для ΔBAD, тогда по теореме ΔBAD - равнобедренный. Так как AD - биссектриса, то ∠BAO = ∠DAO = ∠BAD : 2 = 60° : 2 = 30°, так как ΔBAD равнобедренный, то AB = AD = 10 см. По свойству равнобедренного треугольника если биссектриса является медианой, то она является и высотой, тогда

sin ∠BAO =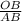 ⇒ OB = AB * sin ∠BAO = 10 * 0,5 = 5 см.