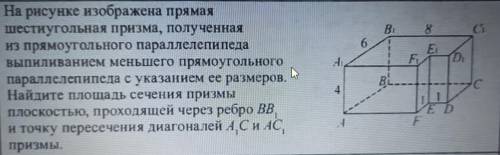
На рисунке изображена прямая шестиугольная призма, полученная из прямоугольного параллелепипеда выпиливанием меньшего прямоугольного параллелепипеда с указанием ее размеров...
Другие вопросы по теме Геометрия
Популярные вопросы
- Персонажами каких басен являются: осел, ворона....
1 - На какой из подчёркнутых вопросов можно ответить как да так и нет? а.. да вместе...
2 - Определите долю городского населения в % от общей численности населения северо-западного...
3 - Учебник по информатике, набранный на компьютере, содержит 256 страниц, на каждой...
1 - On the right i can see a bookcase (special questions)...
2 - Решить цепочку! k - k2o - koh - kcl...
3 - Составьте уравнение окружности с центром в заданной точки о и данным радиусом...
3 - Как проверить вторую е в слове определяет?...
2 - Вкаком предложении вместо слова земляной нужно употребить землистый...
3 - Перевести с казахского на слова жаушы ,күндеме ,шегініп ,көз көріп ,құлақ естімеген...
1
Рассмотрим параллелепипед ABCGA1B1C1G1.
Диагонали параллелепипеда пересекаются в одной точке и делятся это точкой пополам.
=> искомое сечение лежит в плоскости BB1G1G.
△ABG: BG=√(AB^2+AG^2) =10
Пусть BG пересекает прямую FE в точке K.
Искомое сечение - прямоугольник BB1K1K.
△FKG~△ABG, KG/BG =FG/AG =1/8
=> BK =7/8 BG =35/4
S(BB1K1K) =BK*BB1 =35