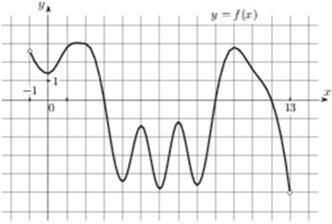
На рисунке изображён график функции y = f(x). Какие из следующих утверждений верны? В ответ запишите номера выбранных утверждений в порядке возрастания без пробелов, запятых и других дополнительных символов.

1. На промежутке (2; 4) знак функции не меняется.

2. На промежутке (-1; 0) функция убывает, на промежутке (0; 1) возрастает.

3. Точка x = 3 является максимумом функции.

4. Функция не является ни четной, ни нечетной.

5. Функция является периодической.

Давайте рассмотрим каждое утверждение по порядку:

1. Утверждение "На промежутке (2; 4) знак функции не меняется" - верно. На данном промежутке график функции расположен выше оси x, что означает, что значения функции положительны.

2. Утверждение "На промежутке (-1; 0) функция убывает, на промежутке (0; 1) возрастает" - неверно. На промежутке (-1; 0) функция возрастает (график идет вверх), а на промежутке (0; 1) функция убывает (график идет вниз).

3. Утверждение "Точка x = 3 является максимумом функции" - невозможно определить только по графику. Для определения экстремумов функции необходимо знать ее производную, что на графике не указано. По графику мы можем только предположить, что точка x = 3 может быть экстремумом функции, но для точного ответа нам нужны дополнительные данные.

4. Утверждение "Функция не является ни четной, ни нечетной" - верно. Четная функция симметрична относительно оси y, то есть f(x) = f(-x). Нечетная функция симметрична относительно начала координат, то есть f(x) = -f(-x). На графике данной функции нет оси симметрии, поэтому она не является ни четной, ни нечетной.

5. Утверждение "Функция является периодической" - неверно. Периодическая функция имеет определенный период, т.е. для любого значения х, f(x) = f(x + T), где Т - период функции. На графике данной функции нет повторяющихся участков, что указывает на отсутствие периодичности.

Итак, верными утверждениями являются 1 и 4. В ответе запишем номера выбранных утверждений в порядке возрастания: 14.