На рисунке даны векторы. Известно, что сторона клетки равна 3 ед. изм. Определи скалярное произведение векторов:
1. u→⋅v→=
;
2. a→⋅m→=
;
3. d→⋅u→=
.
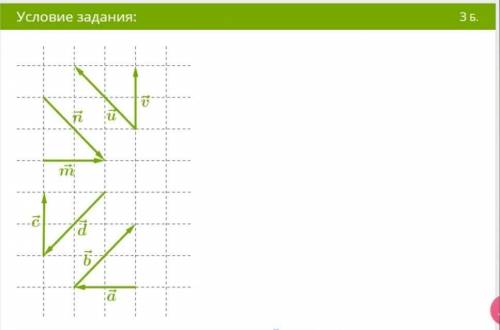
Ответы
Привет! Я буду играть роль школьного учителя и помочь тебе решить эту задачу.
Для определения скалярного произведения векторов, нам нужно умножить соответствующие компоненты этих векторов и сложить результаты. Давай разберемся по очереди.
1. Для начала, нам нужно выразить векторы в координатном виде. Пусть вектор u→ имеет координаты (x1, y1), а вектор v→ имеет координаты (x2, y2).
На рисунке видно, что начало вектора u→ совпадает с координатой (2, 1), а конец - (6, 1). Это означает, что x1 = 6 - 2 = 4, а y1 = 1 - 1 = 0.
Аналогично, для вектора v→ начало совпадает с координатой (4, 1), а конец - (4, 5). Получаем x2 = 4 - 4 = 0, а y2 = 5 - 1 = 4.
Теперь у нас есть координаты векторов: u→(4, 0) и v→(0, 4).
Чтобы найти скалярное произведение, перемножим соответствующие компоненты и сложим результаты:
u→⋅v→ = 4*0 + 0*4 = 0 + 0 = 0.
Ответ: скалярное произведение векторов u→ и v→ равно 0.
2. Теперь давай рассмотрим векторы a→ и m→. Следуя тому же методу, найдем их координаты.
На рисунке видно, что начало вектора a→ совпадает с координатой (2, 4), а конец - (4, 2). Это означает, что x1 = 4 - 2 = 2, а y1 = 2 - 4 = -2.
Аналогично, для вектора m→ начало совпадает с координатой (4, 2), а конец - (1, 1). Получаем x2 = 1 - 4 = -3, а y2 = 1 - 2 = -1.
Теперь у нас есть координаты векторов: a→(2, -2) и m→(-3, -1).
Посчитаем скалярное произведение, умножив соответствующие компоненты и сложив результаты:
a→⋅m→ = 2*(-3) + (-2)*(-1) = -6 + 2 = -4.
Ответ: скалярное произведение векторов a→ и m→ равно -4.
3. Наконец, рассмотрим векторы d→ и u→. Опять же, найдем их координаты.
На рисунке видно, что начало вектора d→ совпадает с координатой (1, 1), а конец - (4, 4). Это означает, что x1 = 4 - 1 = 3, а y1 = 4 - 1 = 3.
Аналогично, для вектора u→ начало совпадает с координатой (2, 1), а конец - (6, 1). Получаем x2 = 6 - 2 = 4, а y2 = 1 - 1 = 0.
Теперь у нас есть координаты векторов: d→(3, 3) и u→(4, 0).
Посчитаем скалярное произведение, умножив соответствующие компоненты и сложив результаты:
d→⋅u→ = 3*4 + 3*0 = 12 + 0 = 12.
Ответ: скалярное произведение векторов d→ и u→ равно 12.
Надеюсь, это помогло! Если у тебя есть еще вопросы, не стесняйся задавать.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Популярные вопросы
- Исследовать и схематично построить график функции y=−x3x2−4...
3 - Moscow is the capital of Russia. It isthe biggest city in the country...
1 - примера когда в обществе меняются критерии стратификации...
1 - Я первую часть сделала (то есть задание 2) но 3 задачу не могу. Я прикрепила...
3 - Решите 2 интеграла, подробно...
1 - ― Любовь ― материя тонкая, и её голыми руками не возьмёшь, — протрубил...
1 - Укажіть твердження, які правильно характеризують поняття гідросфера :...
2 - составить условие уравнения (502-2)*а=1000...
2 - В равностороннем треугольнике проведена медиана АМ - 11 см.Рассчитай расстояние...
2 - Назовите основные качества составляющие природу человека Какое качество...
2