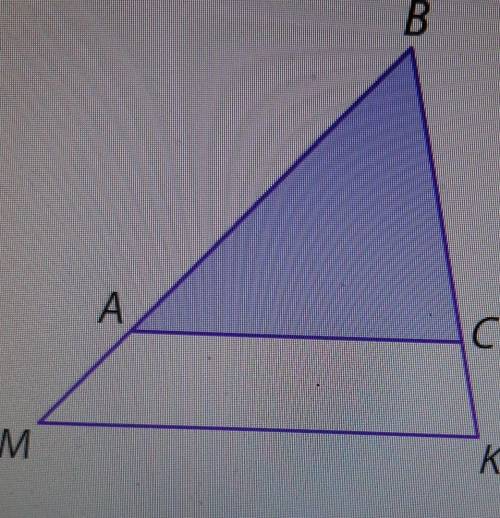
На рисунке BK = 12, CK = 3, AB = 12, MA = 4, AC = 15. Найдите MK ​

Объяснение:

незнаю вообще незнаю вообще

Давайте разберемся с данным вопросом.

Из заданной информации, на рисунке видно, что треугольник ABC является прямоугольным треугольником, так как прямой угол образуется между отрезками AB и AC.

Также, из рисунка видно, что точка K находится на отрезке BC.

Мы хотим найти длину отрезка MK, поэтому нам нужно найти длину отрезка BC, отрезка BK и отрезка MC.

Для начала, используем теорему Пифагора, которая утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Применяя эту теорему к треугольнику ABC, мы можем записать следующее:

AB^2 + AC^2 = BC^2

Подставляя известные значения, получим:

12^2 + 15^2 = BC^2

144 + 225 = BC^2

369 = BC^2

Теперь найдем длину отрезка BC, взяв квадратный корень из обеих сторон уравнения:

sqrt(369) = sqrt(BC^2)

19.24 ≈ BC

Теперь, зная длину отрезка BC, мы можем найти длину отрезка BK.

Из рисунка видно, что отрезок BK является поперечником треугольника ABC, разделяющим его на два прямоугольных треугольника.

Мы можем использовать теорему Пифагора, чтобы найти длину отрезка BK.

Применяя теорему Пифагора к треугольнику ABK, мы можем записать следующее:

AB^2 = AK^2 + BK^2

Подставляя известные значения, получим:

12^2 = 4^2 + BK^2

144 = 16 + BK^2

128 = BK^2

Теперь найдем длину отрезка BK, взяв квадратный корень из обеих сторон уравнения:

sqrt(128) = sqrt(BK^2)

11.31 ≈ BK

И, наконец, используя ранее найденные значения отрезков BK и BC, мы можем найти длину отрезка MC, вычитая длины отрезков BK и BC:

MC = BC - BK
MC ≈ 19.24 - 11.31
MC ≈ 7.93

Теперь мы можем добавить длины отрезков BK и MC, чтобы найти длину отрезка MK:

MK = BK + MC
MK ≈ 11.31 + 7.93
MK ≈ 19.24

Таким образом, мы получаем, что длина отрезка MK примерно равна 19.24.