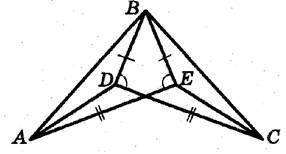
На рисунке BD = BE, DC = AE, ∠BDC = ∠BEA. Найдите длину отрезка AD, если СЕ = 6 см. ответ запишите в сантиметрах.

ответ:снизу (отметь как лучший

Объяснение:

6

тест

Чтобы решить эту задачу, мы можем использовать свойство равных углов и равных отрезков.

Исходя из условия, мы знаем, что BD = BE, DC = AE и ∠BDC = ∠BEA.

Из свойства равных отрезков следует, что AB = AC, так как DB = EB, а DC = AE.

Также из свойства равных углов следует, что ∠ABC = ∠ACB, так как ∠BDC = ∠BEA.

Теперь давайте рассмотрим треугольник ACE. Мы знаем, что AC = AB, так как AB = AC. Также из условия мы знаем, что CE = 6 см.

Из этих данных мы можем заключить, что треугольник ACE является равнобедренным, так как AC = AB и CE = 6 см.

В равнобедренном треугольнике высота, проведенная из вершины, делит основание пополам. Поэтому мы можем заключить, что DE = EC / 2, так как DE является высотой, проведенной из вершины E.

Теперь мы можем продолжить решение задачи, используя информацию о треугольнике BDC. Мы знаем, что BD = BE, а DE = EC / 2. Значит, DB = EC / 2 + EC / 2 = EC.

Теперь мы знаем, что DB = DC и треугольник BDC является равнобедренным, так как DB = DC.

В равнобедренном треугольнике две боковые стороны равны. Поэтому мы можем заключить, что ∠BCD = ∠BDC.

Теперь давайте рассмотрим треугольник BCA. Мы знаем, что ∠ABC = ∠ACB, ∠BCD = ∠BDC и AB = AC.

Треугольник BCA у нас равнобедренный, так как два угла и две стороны равны.

Из свойств равнобедренных треугольников следует, что высота, проведенная из вершины, делит основание пополам. Поэтому мы можем заключить, что AD = AC / 2, так как AD является высотой, проведенной из вершины A.

Мы знаем, что AC = AB и получили ее из условия.

Таким образом, AD = AC / 2 = AB / 2.

Из этого следует, что AD = 6 / 2 = 3 см.

Итак, длина отрезка AD составляет 3 сантиметра.