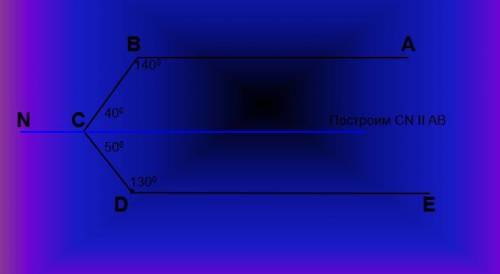
На рисунке АВ II ЕD. (угол) CВА = 140(градусов), (угол)СDE = 130(градусов)
Докажите, что ВС⊥СD

Для доказательства, что BC ⊥ CD, мы можем использовать два свойства параллельных прямых, а именно, что если выполняется одно из следующих условий, то выполняется и другое:
1. Если две прямые параллельны и пересекаются третьей прямой, то сумма смежных углов равна 180 градусов.
2. Если сумма смежных углов равна 180 градусов, то две прямые параллельны.

Давайте рассмотрим рисунок и дадим подробное объяснение.

У нас есть две параллельные прямые: АВ и ED. Мы знаем, что угол CВА равен 140 градусам, а угол СDE равен 130 градусам.

Первым шагом, мы можем заметить, что угол CВА и угол СDE - это смежные углы, так как они находятся по одну сторону и общую сторону угла C.

Вторым шагом, мы можем применить свойство смежных углов, которое гласит: если смежные углы образуются двумя пересекающимися прямыми и сумма этих углов равна 180 градусов, то эти прямые параллельны.

В нашем случае, сумма угла CВА и угла СDE равна 140 градусов + 130 градусов = 270 градусов.

Третьим шагом, мы можем применить второе свойство параллельных прямых, которое гласит: если сумма смежных углов равна 180 градусов, то две прямые параллельны.

В нашем случае, сумма угла CВА и угла СDE больше чем 180 градусов (270 градусов). Таким образом, мы можем сделать вывод, что углы CВА и СDE не могут быть смежными углами и, следовательно, прямые АВ и ED не пересекаются и являются параллельными.

Таким образом, мы сделали вывод, что BC ⊥ CD, то есть BC и CD перпендикулярны друг другу.