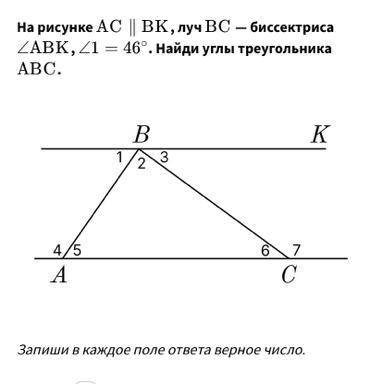
На рисунке AC || BK, луч BC - биссектриса угла ABK, угол 1=46° найди углы треугольника ABC

ответ: А-46°

B-67°

C-67°

Объяснение:

Давайте рассмотрим данную задачу по шагам:

1. По условию задачи, на рисунке AC || BK, что означает, что отрезок AC параллелен отрезку BK. Это значит, что углы ABK и BAC являются соответственными и равны между собой: угол ABK = угол BAC.

2. Также по условию задачи, луч BC является биссектрисой угла ABK. Биссектриса делит угол пополам, значит угол ABK делится на две равные части: угол ABK = угол CBK.

3. Теперь у нас есть два равных угла: угол ABK и угол CBK.

4. Сумма углов в треугольнике равна 180°. Известны углы ABK и CBK, поэтому можно найти третий угол треугольника ABC, используя формулу: угол ABC = 180° - угол ABK - угол CBK.

5. Подставим известные значения углов в формулу: угол ABC = 180° - 46° - угол CBK.

6. Теперь нужно найти значение угла CBK. Мы знаем, что угол 1 равен 46° и угол ABK равен углу CBK. Таким образом, угол ABK = угол CBK = 46°.

7. Подставим найденное значение угла CBK в формулу: угол ABC = 180° - 46° - 46°.

8. Выполним вычисления: угол ABC = 180° - 46° - 46° = 88°.

Ответ: угол ABC равен 88°.