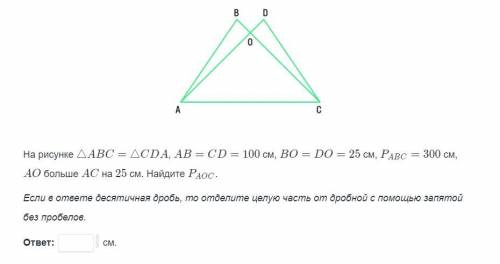
На рисунке ▲ABC=▲CDA, AB=CD=100 см, BO=DO=25 см, Pabc= 300 см, AO больше AC на 25 см. Найдите Paoc

Для решения данной задачи, нам потребуется использовать знания из геометрии и вычисления площадей различных фигур.

Из условия задачи мы знаем, что ▲ABC и ▲CDA являются равными треугольниками, то есть у них равны все стороны и все углы.

Также, по условию мы знаем, что AB = CD = 100 см и BO = DO = 25 см.

Требуется найти площадь фигуры Paoc.

Давайте рассмотрим пошаговое решение задачи:

Шаг 1: Найдем площадь ▲ABC:
Поскольку ▲ABC - равносторонний треугольник со стороной 100 см, мы можем использовать формулу для вычисления площади равностороннего треугольника: S = (a^2 * √3) / 4, где a - длина стороны.
Подставив a = 100 см в формулу, получим:
S(▲ABC) = (100^2 * √3) / 4 = 2500√3 см^2.

Шаг 2: Найдем площадь ▲CDA:
Так как ▲CDA также является равносторонним треугольником со стороной 100 см, его площадь равна S(▲ABC) = 2500√3 см^2.

Шаг 3: Найдем площадь четырехугольника ABCD:
Так как ▲ABC = ▲CDA, то площадь четырехугольника ABCD равна сумме площадей ▲ABC и ▲CDA: S(ABCD) = S(▲ABC) + S(▲CDA) = 2500√3 + 2500√3 = 5000√3 см^2.

Шаг 4: Найдем площадь треугольника Paoc:
Чтобы найти площадь любого треугольника, нам необходимо знать длины его сторон и высоту, опущенную на одну из сторон.
Обратим внимание, что треугольник Paoc находится внутри четырехугольника ABCD, и BO является высотой, опущенной на сторону AC.

Высота треугольника Paoc равна BO = 25 см, а основание треугольника AC равно AO + OC, где AO больше AC на 25 см.

Основание треугольника AC:
AO = AC + 25 см

OC = CD - DO = 100 - 25 = 75 см

AO + OC = AC + 25 + 75 = AC + 100

Так как AO больше AC на 25 см, то получаем уравнение:
AC + 25 + AC = AC + 100

Решим уравнение:
2 * AC + 25 = AC + 100
AC = 75 см

Теперь, когда мы знаем длину сторон треугольника Paoc и его высоту, мы можем найти его площадь, используя формулу для площади треугольника: S = (a * h) / 2, где a - длина основания треугольника, h - высота.
Подставим значения:
S(Paoc) = (75 * 25) / 2 = 1875 см^2.

Ответ: Площадь треугольника Paoc равна 1875 см^2.