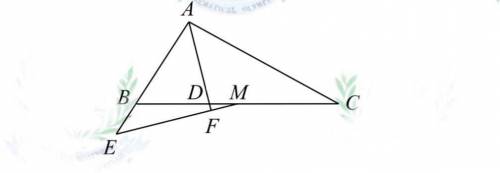
На рисунке ∠ABC=2∠ACB ; ∠BAD=∠CAD ; M середина BC ; AF⊥EM . Если BE=1 .
Найдите BD =?

Построим △AB1C1, симметричный △ABC относительно биссектрисы AD

(точки B1 и C1 на сторонах AC и AB соответственно)

∠C1=∠C =∠ABC/2

∠BDC1 =∠ABC-∠C1 =∠C1 (∠ABC - внешний угол в △C1BD)

=> △C1BD - р/б, BC1=BD

EM⊥AD => EM||CC1 => BE/EC1 =BM/MC=1/1 (т Фалеса)

Тогда BС1 =2BE =2 =BD