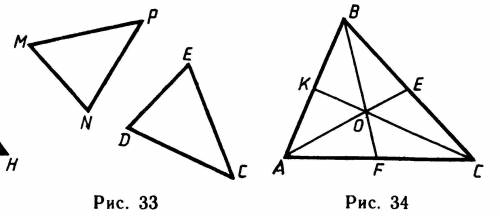
на рисунке ! 33 ! изображены треугольники MNP и CDE у которых угол M = углу D, MN=DE. Докажите что угол E = углу N, если MP=CD
Другие вопросы по теме Геометрия
Популярные вопросы
- Write the number. 1 one thousand seven hundred and fifte.2. six thousand....
2 - По двум параллельным железнодорожным путям равномерно движутся два...
1 - За какое время тело движущееся с ускорением 0,5 МС квадрат из состояния...
1 - уже через полчаса сдаватьЗадачи 3 и 5 >...
2 - Постройте график функции y=3x+4 и укажите координаты точек пересечения...
2 - 2. Які країни претендували на українські землі напередодні та під...
2 - 5. Вычислите: arccos (sin 10) Даны функции: f(x) = 2х – 1 ф(t) = t2...
1 - Назовите страны бассейна 1)реки Параны 2)реки Юкон 3)реки Нил...
2 - Найти перпендикулярную плоскость...
3 - Задача 2 Сторона AB паралелограма ABCD належить площині а, а сторона...
2
Дано: треугольники MNP и CDE, где угол M = углу D, MN = DE, а также MP = CD.
1. По условию задачи, угол M = углу D.
2. MN = DE, что означает, что сторона MN равна стороне DE.
3. Также MP = CD.
Требуется доказать, что угол E = углу N.
Доказательство:
1. Из условия задачи имеем равенство углов M и D.
2. Заметим, что угол N является внутренним углом треугольника MNP, а угол E является внутренним углом треугольника CDE.
3. Рассмотрим треугольникы MNP и CDE.
4. У нас есть два равных угла (M = D) и две равные стороны (MN = DE, MP = CD) в этих треугольниках.
5. Используя аксиому о равенстве треугольников по двум углам и стороне между ними, мы можем сделать вывод, что треугольники MNP и CDE равны.
6. Следовательно, углы N и E также равны.
7. Таким образом, мы доказали, что угол E = углу N.