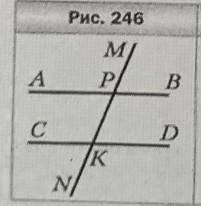
На рисунке 246 прямые АВ и CD параллельны. Докажите, что биссектрисы углов АРМ и DKN параллельны.​

ответ на вложении, можно лучший ответ:33

Чтобы доказать, что биссектрисы углов АРМ и DKN параллельны, мы можем использовать свойство параллельных прямых и углы с параллельными сторонами. Давайте разберемся пошагово.

1. Дано: На рисунке 246 прямые AB и CD параллельны (задано на рисунке).

2. Предположение: Докажем, что биссектрисы углов АРМ и DKN параллельны.

3. Доказательство:

- Рассмотрим треугольник ARM. Поскольку прямые AB и CD параллельны, то угол PAR является вертикально противолежащим углу RDK (вертикальные углы равны).

- Из вертикальных углов PAR и RDK следует, что они равны между собой (по определению вертикальных углов).

- Расмотрим биссектрису угла ARM, обозначим ее как AM1. Так как AM1 делит угол ARM пополам, то угол PAM1 равен углу RAM (по определению биссектрисы).

- Аналогично, рассмотрим треугольник DNK. Угол PDK равен углу PKD, так как они являются вертикально противолежащими углами.

- Рассмотрим биссектрису угла DKN, обозначим ее как DK1. Угол PDK1 равен углу DK1K, так как DK1 делит угол DKN пополам.

- Теперь сравним углы PAM1 и PDK1. Они равны углам RAM и PKD соответственно, так как они являются биссектрисами соответствующих углов.

- Мы знаем, что углы RAM и PKD равны, поэтому углы PAM1 и PDK1 также равны.

- Из последнего пункта мы можем сделать вывод, что биссектрисы углов АРМ и DKN параллельны (если два угла одного треугольника равны двум углам другого треугольника, то стороны, от которых эти углы отсчитываются, параллельны).

4. Заключение: Мы доказали, что биссектрисы углов АРМ и DKN параллельны.

Надеюсь, это доказательство понятно для вас и помогло вам понять, почему биссектрисы указанных углов параллельны.