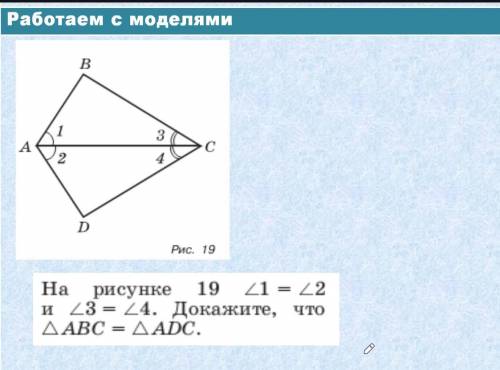
На рисунке 19 /1 = /2 и /3 = /4. Докажите, что = /ABC =/ADC.

Для начала давайте рассмотрим, что означают данные углы на рисунке.

На рисунке дано, что угол /1 равен углу /2, а угол /3 равен углу /4. То есть, мы имеем следующие равенства:

/1 = /2 (условие 1)
/3 = /4 (условие 2)

На рисунке также указано, что отрезок АВ равен отрезку CD. То есть, имеем следующее равенство:
АВ = CD

Теперь наша задача доказать, что угол /ABC равен углу /ADC.

Давайте рассмотрим треугольник АВС и треугольник СДС.

У этих треугольников есть следующие общие элементы:
1. Они оба имеют общую сторону - сторону С.
2. У них есть общий угол - угол /C, так как он находится в самом треугольнике ABC и в самом треугольнике ADC.

Также, у этих треугольников нет равных сторон или равных углов, кроме общего угла /C. То есть, треугольники АВС и СДС являются подобными треугольниками (по свойству подобных треугольников).

Известно, что отношение длин соответствующих сторон подобных треугольников равно. То есть, если треугольники АВС и СДС подобны, то отношение длин их сторон такое:

AB / AC = CD / CS

Теперь давайте рассмотрим отношение длин отрезков АВ и CD по условию:

AB = CD

Подставим это в предыдущее уравнение:

AB / AC = AB / CS

Теперь обратимся к свойству отношения длин сторон треугольника: отношение длины стороны к длине прилежащей стороны равно отношению синуса угла, противолежащего первой стороне, к синусу угла, противолежащего второй стороне. Применим это свойство для треугольника АВС:

AB / AC = sin(/ABC) / sin(/BAC)

И для треугольника СДС:

CD / CS = sin(/ADC) / sin(/CDS)

Так как /1 и /2 равны, то и /BAC = /CDS. Также, по условию /3 = /4, что значит, что /ABC = /ADC.

Итак, имеем следующее:

AB / AC = AB / CS
sin(/ABC) / sin(/BAC) = sin(/ADC) / sin(/CDS)

Так как все углы А, /BAC, /ABC, /CDS и /ADC лежат в одной плоскости, было бы удобно воспользоваться теоремой синусов для треугольника ABC:

AB / sin(/ABC) = AC / sin(/BAC)

И для треугольника CDA:

CD / sin(/ADC) = CS / sin(/CDS)

Так как AB = CD по условию, а также sin(/ABC) / sin(/BAC) = sin(/ADC) / sin(/CDS), можно сделать следующие выводы:

AB / sin(/ABC) = CD / sin(/ADC) ---- (1)
AB / AC = CD / CS ---- (2)

(1) и (2) являются одинаковыми выражениями, поэтому:

AB / sin(/ABC) = AB / AC

Отбросим общий множитель AB:

1 / sin(/ABC) = 1 / AC

Сократим обе части на 1:

1/sin(/ABC) = 1/AC

или

sin(/ABC) = AC

Таким образом, мы доказали, что у нас есть равенство:

sin(/ABC) = AC

Теперь, заметим, что sin(/ABC) равно sin(/ADC), так как /ABC = /ADC по условию.

То есть, получаем:

sin(/ADC) = AC

Поскольку мы знаем, что sin(/ADC) равно AC, то мы можем сделать следующий вывод:

AC = AC

Таким образом, мы доказали, что сторона АС равна самой себе, что является тождественным утверждением.

Таким образом, мы доказали, что угол /ABC равен углу /ADC на основе данных равенств и свойств подобных треугольников.