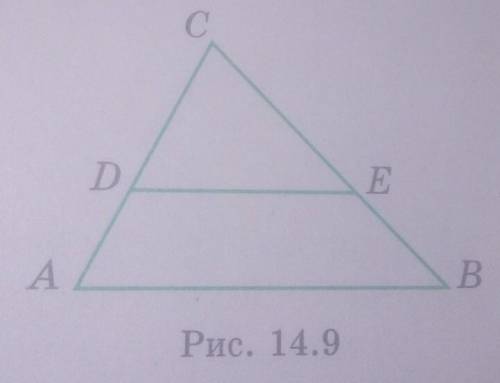
На рисунке 14.9 DE=10, CE=8, BC=12, угол BAC равен углу EDC. Найдите AB
РЕШИТЕ ПОБЫСТРЕЕ ОЧЕНЬ НУЖНО (И ПУСТЬ ОТВЕТ БУДЕТ РАЗВЁРНУТЫЙ) ​

Для решения данной задачи, нам понадобится знание треугольников и углов.

Из условия задачи мы знаем, что угол BAC равен углу EDC. Поскольку эти углы равны, то мы можем заключить, что треугольники ABC и ECD подобны, так как имеют одинаковые углы.

Теперь, чтобы найти значение AB, мы можем использовать пропорциональные стороны треугольников ABC и ECD.

Сравнивая соответствующие стороны AB и DE в этих треугольниках, мы можем записать следующее уравнение пропорции:

AB / DE = BC / CE

Подставляя известные значения, получим:

AB / 10 = 12 / 8

Для решения этого уравнения сначала умножим обе части на 10, чтобы избавиться от знаменателя:

AB = (12 / 8) * 10

Выполним вычисления:

AB = 1.5 * 10

AB = 15

Таким образом, длина AB равна 15 единицам.