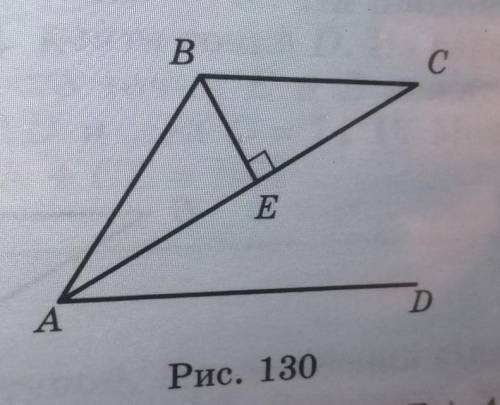
На рисунке 130 AC биссектриса угла BAD, BE I AC
и AE = ЕС. Докажите, что AD II ВС.
Другие вопросы по теме Геометрия
Популярные вопросы
- Обзор любого средства массовой информации...
2 - Вырази: а) в секундах-3 мин; 20 мин; 100 мин; 4 мин 20 с; б) в килограммах-2 т...
3 - Всё ли ясно в телеграмме? исправьте текст....
3 - Один килограмм конфет дороже килограмма печенья на 2,6 рублей. за 8 кг конфет...
1 - Два одинаковых конденсатора емкостью 3мкф соединили параллельно и зарядили до...
2 - Какие причины приводили к продвижению в сибирь?...
3 - Напряжение на учатске цепи 100в,его сопративление 200 ом.какова мощность тока...
2 - Яку масу рослин зберігає пара синиць при вигодовуванні 4 пташенят вагою по 5г...
1 - Мини сочинение. мое отношение к маяковскому как к поэту и как к человеку...
1 - Вряду na-mg-al-si металлические свойства 1) усиливаются 3) не изменяются 2) ослабевают...
1
1. Дано, что AC является биссектрисой угла BAD. Это означает, что AC делит угол BAD на два равных угла.
2. Дано также, что BE || AC и AE = EC. Здесь мы имеем параллельные прямые и равенство отрезков.
Теперь рассмотрим следующие углы:
Угол BAE: Этот угол равен половине угла BAD, так как AC является биссектрисой угла BAD.
Угол AEC: Этот угол также равен половине угла BAD, поскольку AE = EC и BE || AC, что означает, что AEС является равнобедренным треугольником.
Угол AEB: Этот угол является вертикальным углом с углом BAD и, следовательно, также равен половине угла BAD.
Из наших рассуждений следует, что угол BAE, AEC и AEB равны между собой, так как они все являются половинами угла BAD.
Теперь рассмотрим треугольники ABD и ACB. У нас есть следующие равенства углов:
Угол BAD: Это угол между прямыми AD и ВС.
Угол BCA: Это угол между прямыми BC и AC.
Из равенства углов BAE и AEC следует, что угол BAE = угол AEC.
Из равенства углов AEB и BCA следует, что угол BAE = угол AEB.
Из данных равенств можно сделать вывод, что угол AEB = угол BCA.
Теперь мы можем использовать свойство параллельных прямых.
Если две параллельные прямые пересекаются с третьей прямой, то соответствующие углы на одной стороне от пересекающей прямой будут равны.
Из равенства углов AEB и BCA следует, что угол ABD = угол ACB.
Таким образом, углы ABD и ACB равны соответственно на одной стороне от пересекающей прямой AC.
Но эти углы также являются внутренними углами треугольников ABD и ACB.
Таким образом, эти треугольники должны быть подобными.
Внутренние углы треугольников одинаковы, следовательно, соответствующие стороны параллельны.
Таким образом, AD || ВС, что и требовалось доказать.