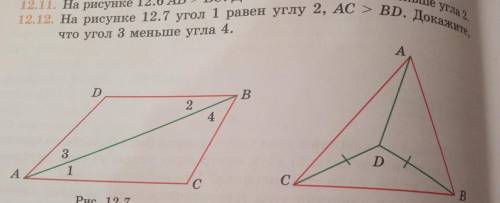
На рисунке 12 7 угол один равен углу два AC больше чем BD Докажите что угол 3 меньше угла 4

Для доказательства того, что угол 3 меньше угла 4, мы должны использовать информацию, представленную на рисунке и применять основные геометрические принципы.

Из условия задачи известно, что угол один равен углу два, и что AC больше, чем BD. Мы можем использовать эти факты для доказательства.

Во-первых, посмотрим на треугольник ABC. Мы можем заметить, что угол 1 и угол 3 образуют вертикальные углы, и поэтому они равны друг другу. Таким образом, угол 1 равен углу 3.

Теперь рассмотрим треугольник BCD. У нас есть две прямых линии, AC и BD, которые пересекаются в точке B. По условию известно, что AC больше, чем BD. Это означает, что угол 2 больше, чем угол 4, так как количество градусов в угле зависит от длины соответствующей стороны: чем больше сторона, тем больше угол.

Таким образом, мы получаем, что угол 2 больше, чем угол 4.

Так как угол 1 равен углу 3, и угол 2 больше, чем угол 4, то мы можем заключить, что угол 3 меньше угла 4.

Таким образом, мы доказали, что угол 3 меньше, чем угол 4, используя информацию и принципы геометрии, представленные в задаче.