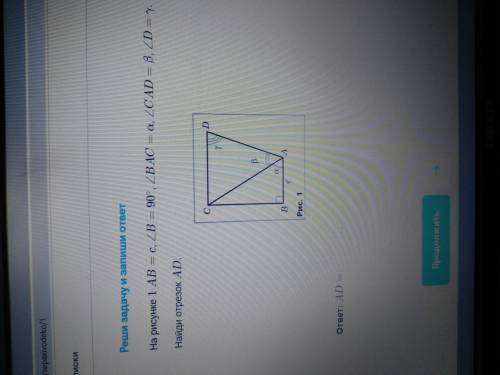
На рисунке 1 АВ=с, угол В=90°, угол ВАС=а, угол САD=в, угол D=у. Найдите отрезок АД.

Для решения данной задачи, мы будем использовать основные свойства треугольников и тригонометрические соотношения.

1. Из рисунка видно, что угол ВАС является прямым углом, так как угол В равен 90°.

2. Рассмотрим треугольник AВС. У нас есть информация о длине стороны АВ (с), значении угла ВАС (а) и угле САD (в). Мы хотим найти длину отрезка АД.

3. Обозначим точку Е на продолжении отрезка АВ за пределы треугольника AВС так, чтобы сегмент АЕ был параллелен отрезку СD. Теперь у нас есть правильный прямоугольный треугольник BCE.

4. Рассмотрим треугольник BCE. Так как угол D (у) расположен на прямой продолжении отрезка AD, то он также является прямым углом.

5. Обратимся к тригонометрическим соотношениям в прямоугольном треугольнике BCE:

тангенс угла D (у) = противолежащий катет (AC) / прилежащий катет (EC).
Катет AC - это отрезок AD, который мы хотим найти, а катет EC - это отрезок CD.

Итак, тангенс у = AC / EC.

6. Мы можем найти значение тангенса угла D (у) с помощью тригонометрической функции тангенса:
тангенс у = tan(у).
Зная значение угла D (у), мы можем найти значение тангенса.

7. Когда мы найдем значение тангенса угла D (у), мы можем записать соотношение:
тангенс у = AC / EC.

8. Мы знаем, что катет EC равен стороне СD, которая равна с (см. условие задачи). Мы также знаем значение угла D (в), которое также указано в условии задачи.

9. Таким образом, у нас есть два уравнения:
тангенс у = AC / c (уравнение 1),
угол D = в (уравнение 2).

10. Мы можем решить уравнение 1 для AC:
AC = c * тангенс у.

11. Теперь мы можем подставить это значение AC в уравнение 2 и решить уравнение относительно угла у:
в = arctan(AC / c).

12. Решив это уравнение, мы найдем значение угла D (у) в радианах.

13. Наконец, мы можем использовать найденное значение угла D (у), чтобы найти длину отрезка AD, используя соотношение:
AC = AD = c * тангенс у.

Итак, чтобы найти длину отрезка АД, мы должны вычислить тангенс угла D (у), используя данные в условии задачи, и затем умножить результат на длину стороны АВ (с).