На рис 44 АВСD - параллелограмм, ВЕ перпендикулярно АD, АЕ=3см,СD=5cм, ВС=10см найдите S abcd

Ответы

арина256545 15.02.2022 01:40

40cm^2

Объяснение:

/ | /

A/__|___/D

$S_{abcd}=ah=AD*BE$

BC=10 см

AD=BC (в параллелограмме противолежащие стороны равны)

СD=5 см

AB=CD

Треугольник ABE прямоугольный, т.к. ВЕ перпендикулярно АD

Значит BE=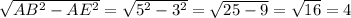 $\sqrt{AB^2-AE^2}=\sqrt{5^2-3^2}=\sqrt{25-9}=\sqrt{16} =4$ см

$S_{abcd}=10*4=40 cm^2$

ПОКАЗАТЬ ОТВЕТЫ

starkoviv23 21.01.2024 17:49

Хорошо, давайте решим эту задачу пошагово.

1. Для начала, давайте определим, какие данные нам даны в задаче:
- ВЕ является перпендикуляром к АД.
- Длина АЕ равна 3 см.
- Длина СD равна 5 см.
- Длина ВС равна 10 см.

2. Согласно условию, рисунок АВСD образует параллелограмм. Это означает, что сторона СD параллельна стороне AB и имеет такую же длину.

3. Также, по свойству параллелограмма, ВЕ является высотой, опущенной на сторону АД. Это означает, что длина ВЕ является высотой параллелограмма и перпендикулярна стороне АД.

4. Теперь мы можем использовать эти данные, чтобы решить задачу. Для начала, найдем высоту параллелограмма.

5. По определению, площадь параллелограмма равна произведению его высоты на длину одной из его сторон. В нашем случае, высота параллелограмма - это ВЕ, а длина одной из сторон - это СD. Таким образом, S(ABCD) = ВЕ * СD.

6. Мы знаем, что ВЕ = 3 см и СD = 5 см, поэтому мы можем подставить эти значения в формулу: S(ABCD) = 3 см * 5 см.

7. Чтобы найти площадь, мы должны перемножить 3 и 5: S(ABCD) = 15 см².

Итак, площадь параллелограмма ABCD равна 15 см².

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия