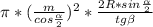На расстоянии m от оси цилиндра проведено сечение, параллельное оси и отсекающее от окружности основания дугу альфа. диагональ сечения пересекается с образующей цилиндра под углом бетта. найдите объем цилиндра.
Другие вопросы по теме Геометрия
Популярные вопросы
- (2х+3)^2+11=12(2х^2+3) решения...
1 - При каких значениях x двучлен 5x−7 принимает отрицательные значения?...
3 - Как мне сфоткать во Помигите...
2 - 200-210 найти производную функции...
1 - Индивидуальный предприниматель Фролова была привлечена к ответственности...
1 - Развенчание идеал наполеонизма ...
3 - Что нужно сделать, чтобы в природе сохранялись сибирские орхидеи...
3 - Укажи строчку(-и), в которой(-ых) все глаголы стоят в изъявительном...
1 - ОЧЕНЬ Найдите предложения с обособленными членами. Выпишите их....
2 - Когда появились первые признаки жизни на Земле?Когда появился первобытный...
3
V =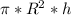
найдем радиус cos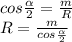
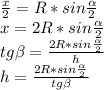
V =