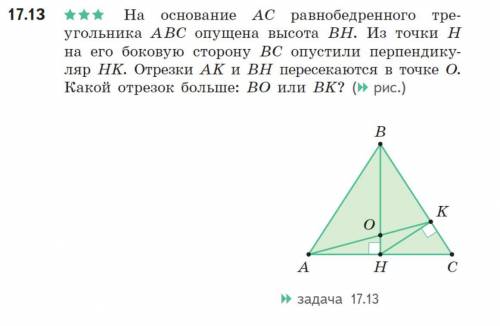
На основании AC равнобедренного треугольника ABC опущена высота BH. Из точки H на его боковую сторону BC опустили перпендикуляр HK. Отрезки AK и BH пересекаются в точке O.
Какой отрезок больше: BO или BK?

Давайте рассмотрим данную ситуацию шаг за шагом.

У нас имеется равнобедренный треугольник ABC, где AC является основанием. Также, мы видим, что на основании AC опущена высота BH. Из точки H на сторону BC опущен перпендикуляр HK. Отрезки AK и BH пересекаются в точке O.

Чтобы ответить на вопрос, какой из отрезков BO и BK больше, давайте рассмотрим некоторые свойства данной фигуры.

Первое, что нам нужно заметить, это то, что треугольник ABC является равнобедренным. Это значит, что стороны AB и AC равны друг другу.

Также, мы видим, что перпендикуляр HK проведен из точки H на сторону BC. Это значит, что треугольники BHK и BAC подобны, поскольку у них имеются два угла, которые совпадают: углы BHK и BAC равны 90 градусам, и углы BKH и BCA равны, так как являются вертикальными углами.

Теперь очень важно заметить, что перпендикуляр HK делит сторону BC пополам, так как BH является высотой равнобедренного треугольника ABC. Это значит, что отрезок BK будет равен отрезку KC.

Таким образом, чтобы узнать, какой из отрезков BO и BK больше, нам нужно сравнить BO и KC.

Чтобы это сделать, мы можем использовать пропорцию треугольников: BHK и BCA.

Мы знаем, что треугольники BHK и BAC подобны. Поэтому, соответствующие стороны относятся как соответствующие стороны другого треугольника.

То есть, мы можем записать пропорцию: BH/KH = BA/AC.

Так как AB и AC равны, мы можем записать пропорцию BH/KH = AB/AC.

Поскольку отрезки AB и KC равны (так как треугольник ABC равнобедренный), мы можем заменить выражение AB/AC значением KC/AC.

Теперь нам нужно сравнить BO и KC. Мы можем сделать это, выразив BO через KC с использованием пропорции, которую мы только что получили.

Мы знаем, что отрезок BO равен отрезку AO минус отрезок AK.

Мы можем выразить отрезок AO через отрезок KC, используя пропорцию BH/KH = AB/AC.

Таким образом, мы получаем BO = (AB * KH)/KH - BK.

Так как KH в числителе и знаменателе сокращаются, мы получаем BO = AB - BK.

Теперь у нас есть равенство BO = AB - BK и мы хотим сравнить BO и KC.

Мы знаем, что AB и KC равны по длине. Теперь, поскольку BO = AB - BK, мы можем заменить AB в этом выражении на KC.

Таким образом, мы получаем BO = KC - BK.

Теперь видно, что BO и KC имеют одинаковое значенние. Они равны, так как AB и KC равны (так как треугольник ABC равнобедренный) и отрезок BK равен отрезку KC (потому что HK делит сторону BC пополам).

В итоге, мы можем заключить, что отрезок BO равен отрезку BK. Они имеют одинаковую длину.

Таким образом, BO и BK одинаковы по длине.