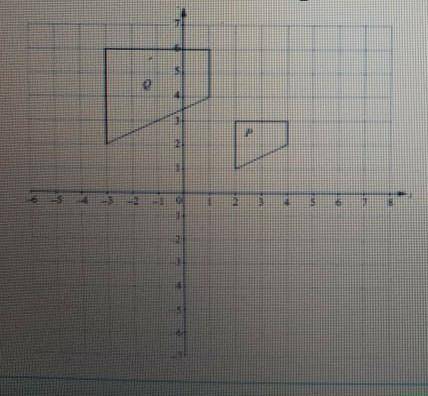
На графике изображены две фигуры P и Q.
a) используя точку (0;-1) в качестве центра поворота, поворачиваем фигуру P по часовой стрелке на 90 градусов. Отметьте полученные изображения R полного исчерпания, затем трафик.
b) скопируйте фигуру, изображенную буквой R, симметрично, чем прямая x=-2. Отметьте полученные изображения L полного исчерпания, затем трафик.
c) перенесите фигуру Q (-1;0) в центр симметрии. Изображения, полученные K, отметьте полного исчерпания, затем трафик.
Другие вопросы по теме Геометрия
Популярные вопросы
- Зачет по 8 класс ! 1.магнитное поле (определение, где существует) 2.магнитные...
2 - Заполните таблицу , подбивая к данным именам существительным имена прилогательные...
3 - Выполни морфологический разбор личного местоимения. указывай признаки в том порядке,...
3 - Луч oc делит угол aob на два угла. найдите угол boc, если aob = 78 градусов...
2 - 1) выражение 1/x +x-2y/2xy и найдите его значение при x=√2+1, y=1/4...
2 - Сочинение по рассказу после . на тему почему иван васильевич разлюбил вареньку...
3 - Как люди должны относится друг к другу в семье...
3 - Найдите координаты точки пересечения графика функции y=4x^2+3x-7 с осью ординат...
1 - Виписати із кобзаря 5 реч. із зворотами...
2 - Сто одинаковых стаканов нада упоковать в коробки по вмещающие 6 стаканов...
3
Формулы поворота точки (x, y) на угол α по часовой стрелке, используя центр поворота (a, b), выглядят следующим образом:
x' = (x-a) * cos(α) - (y-b) * sin(α) + a
y' = (x-a) * sin(α) + (y-b) * cos(α) + b
Где:
- (x', y') - координаты повернутой точки
- (x, y) - координаты исходной точки
- (a, b) - координаты центра поворота
- α - угол поворота (в радианах)
Исходя из этого, для поворота фигуры P на 90 градусов по часовой стрелке относительно центра (0, -1), мы применим формулы поворота к каждой точке фигуры P:
P1(-5, -2):
x' = (-5-0) * cos(90°) - (-2-(-1)) * sin(90°) + 0
y' = (-5-0) * sin(90°) + (-2-(-1)) * cos(90°) + (-1)
P1(-5, -2):
x' = -5 * 0 - 1 * 1 + 0
y' = -5 * 1 + 1 * 0 + (-1)
P1(-5, -2):
x' = 0
y' = -6
Таким образом, координаты точки R1 полученной после поворота фигуры P1 равны (0, -6).
P2(-2, -1):
x' = (-2-0) * cos(90°) - (-1-(-1)) * sin(90°) + 0
y' = (-2-0) * sin(90°) + (-1-(-1)) * cos(90°) + (-1)
P2(-2, -1):
x' = -2 * 0 - 0 + 0
y' = -2 * 1 + 0 + (-1)
P2(-2, -1):
x' = 0
y' = -3
Таким образом, координаты точки R2 полученной после поворота фигуры P2 равны (0, -3).
Получаемые изображения R после поворота фигуры P на 90 градусов по часовой стрелке относительно центра (0, -1) - это точки R1(0, -6) и R2(0, -3).
b) Чтобы скопировать фигуру R симметрично относительно прямой x = -2, мы заменим x-координаты каждой точки на их отрицание и оставим y-координаты неизменными.
То есть, если у нас есть точка R1(0, -6), то ее симметричная точка будет иметь координаты (-2 * (-1), -6), то есть (-2, -6).
Точка R2(0, -3) станет (-2 * (-1), -3), то есть (-2, -3).
Получаемые изображения L после симметричного копирования фигуры R относительно прямой x = -2 - это точки L1(-2, -6) и L2(-2, -3).
c) Чтобы перенести фигуру Q (-1, 0) в центр симметрии, мы просто должны вычесть координаты центра симметрии из координат каждой точки фигуры Q.
То есть:
Q1(-3, 1):
x' = -3 - (-1) = -3 + 1 = -2
y' = 1 - 0 = 1
Таким образом, получаемые изображения K после переноса фигуры Q (-1, 0) в центр (0, 0) - это точка K1(-2, 1).
Изображение: