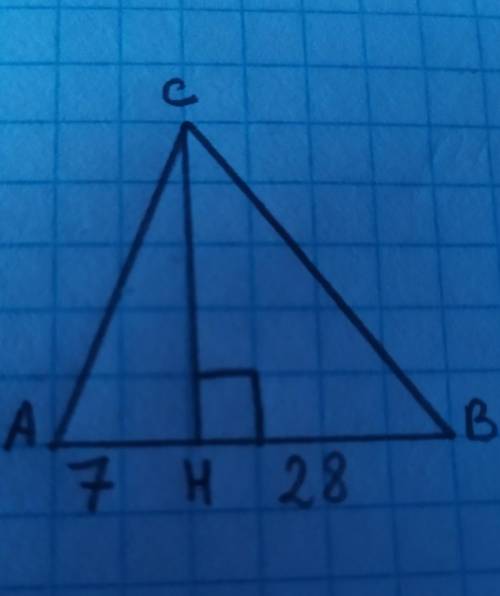
На гипотенузу прямоугольного треугольника ABC опущена высота CH, AH=7, BH=28. найдите CH​

ответ:14 см

Объяснение: по формуле СН^2 =АН*НВ; тогда Сн^2= 7*28=196; корень из 196 =14 см

Чтобы найти длину отрезка CH, нам понадобятся знания о прямоугольных треугольниках и их свойствах. Задача состоит в нахождении длины высоты, которая опущена на гипотенузу треугольника ABC.

Так как треугольник ABC прямоугольный, мы можем использовать теорему Пифагора, которая гласит, что квадрат длины гипотенузы равен сумме квадратов длин катетов. В нашем случае, гипотенуза - это отрезок AC, а катеты - это отрезки AH и BH. Формула теоремы Пифагора выглядит следующим образом:

AC^2 = AH^2 + BH^2

Заменяем известные значения:

AC^2 = 7^2 + 28^2

AC^2 = 49 + 784

AC^2 = 833

Теперь возьмем корень от обеих сторон уравнения, чтобы найти длину AC:

AC = √833

На этом этапе нам непонятно точное значение корня из 833, поэтому оставим ответ таким: AC = √833.

Теперь нам нужно найти длину отрезка CH. Для этого мы можем воспользоваться свойством прямоугольных треугольников, согласно которому высота, опущенная на гипотенузу, делит гипотенузу на две смежные отрезки, длины которых пропорциональны длинам катетов.

Используем этот свойство:

AC/CH = AH/BH

Заменяем известные значения:

√833/CH = 7/28

Теперь решим это уравнение. Сначала упростим его, умножив обе части на CH:

√833 = 7/28 * CH

√833 = 1/4 * CH

Теперь избавимся от знаменателя, умножив обе части на 4:

4 * √833 = CH

Итак, длина отрезка CH равна 4 * √833.

Таким образом, ответ на задачу: CH = 4 * √833.