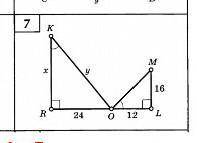
на фото показано что известно, а что нужно найти х и у. Нужно решение.​​

На данной фотографии представлена геометрическая фигура, состоящая из треугольника и двух прямых линий. Условие задачи заключается в том, чтобы найти значения переменных х и у.

Для решения этой задачи, давайте рассмотрим особенности данной геометрической фигуры и вспомним некоторые свойства треугольников.

В данной фигуре видим, что проходит две параллельные прямые линии, обозначенные в задаче AB и CD. Из этого следует, что угол АВС и угол DBC являются соответственно одинаковыми. Это известное свойство параллельных прямых.

Также заметим, что внутренние углы треугольника ABC равны 180 градусам. Используя это свойство, мы можем записать уравнение:

∠BAC + ∠BCA + ∠CAB = 180

Но поскольку ∠BAC и ∠BCA являются соответственно одинаковыми с углами углами АВС и DBC, то мы можем заменить их:

∠ABС + ∠BCA + ∠CAB = 180

Мы также видим, что на фотографии дано значение угла ABC, то есть 80 градусов. Подставим это значение в уравнение:

80 + ∠BCA + ∠CAB = 180

Для дальнейшего решения нам нужно определить, какая информация о геометрической фигуре дана на фотографии, чтобы найти угол BCA или угол CAB.

Найдём угол BCA. Обратимся к прямым линиям AB и CD. Мы видим, что угол ABC и угол CBD являются соответствующими углами, образованными между параллельными прямыми. Из свойств параллельных прямых следует, что эти два угла равны. Поэтому может быть записано уравнение:

∠ABC = ∠BCD

Но на фотографии известное значение угла ABC составляет 80 градусов, поэтому мы можем записать:

80 = ∠BCD

Теперь мы знаем, что угол BCD равен 80 градусов.

Также нам дано, что угол DCE равен 15 градусам. Суммируя это информацию, мы можем выразить угол BCA:

∠BCA = ∠BCD + ∠DCE = 80 + 15 = 95 градусов

Теперь у нас есть значение угла BCA - 95 градусов.

Таким образом, мы решаем задачу о нахождении значений переменных х и у, используя свойства параллельных прямых и свойства углов треугольников.

Чтобы найти значение переменной у, нам нужно рассмотреть треугольник ADC и вспомнить, что сумма углов треугольника равна 180 градусов.

У нас уже есть угол DCE равен 15 градусам и угол DAC, который мы ищем. Подставив эти значения в уравнение:

∠DAC + ∠DCA + ∠CDA = 180

Мы знаем, что угол DCA равен ∠BCA (так как эти углы соответствующие друг другу), то есть 95 градусов:

∠DAC + 95 + 15 = 180

∠DAC = 180 - 95 - 15 = 70 градусов

Теперь мы знаем, что угол DAC равен 70 градусам.

Таким образом, мы решаем задачу о нахождении значений переменных х и у, используя свойства углов треугольников и их суммы равной 180 градусам.

Так как мы нашли значения углов, то можно ответить на вопрос: значение х равно 70 градусам, а значение у равно 95 градусам.