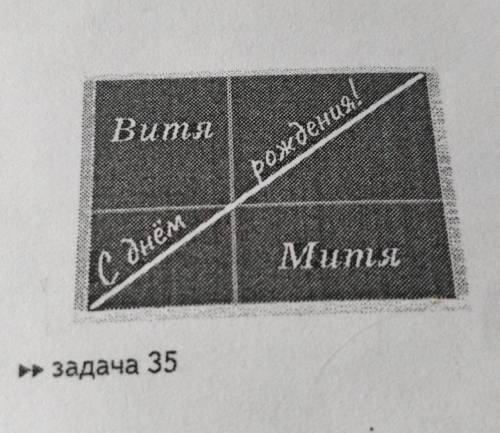
На день рождения близнецы Витя и Митя получили шоколадный торт прямоугольной формы, диагональ кото-рого была проведена белой глазурью. Папа разрезал весь торт на четыре пря-моугольных куска так, как это показанона рисунке. Близнецы терпеть не могутбелой глазури, поэтому они взяли себе тедва куска торта, на которых её больше небыло. На каждом из этих кусков напи-сано имя того мальчика, который его по-лучил. Кому из близнецов досталось больше торта с пояснением решения)
Другие вопросы по теме Геометрия
Популярные вопросы
- Задайте формулу функции, если значение функции: 1)противоположны соответствующим...
3 - Текст: все знают рябину.её красота особенно заметна поздней осенью.листьев на...
3 - 10 примеров значений растений в природе и 10 в жизни человека. заранее !...
2 - Марья морёна какой предмет оставил иван уаревиц...
3 - Решите уравнения: 1) ||x|-4|=2 2)||2x-1|-5|=7...
3 - Сколько минут между 3: 47 и 12: 15? !...
1 - Чтобы заполнить сосуд имеющий форму куба потребовалось 1840 г жидкости. сколько...
2 - Подберите значения a при которых значения 1/a, является положительным дробным...
1 - (5кооней из3+корень из27): корень из 3...
1 - 3мин. 40 сек. = сёк., 6дм7см=,30020г=...
3
Відповідь:
Площадь куска с надписью "Витя" равна площади куска с надписью "Митя".
Пояснення:
Пусть длина торта равна Х = Х1 + Х2, где Х1 - длина левой части ( там где написано "Витя" ), а Х2 - длина правой части ( там где написано "Митя" ).
Пусть ширина торта равна У = У1 + У2, где У1 - ширина верхней части ( там где написано "Витя" ), а У2 - ширина нижней части ( там где написано "Митя" ).
Тогда площадь куска с надписью "Витя" равна S1 = Х1 × У1, а площадь куска с надписью "Митя" равна S2 = Х2 × У2.
Поскольку в прямоугольнике проведена диагональ, то должна выполняться пропорция:
Х / У = Х1 / У2 = Х2 / У1 ( в пропорции индексы 1 и 2 возле Х и У не совпадают, так как мы привязали номера к кускам с именами и взяли номера Х слева на право, а номера У сверху вниз ).
Приведем уравнение для площади куска с надписью "Митя" ( S2 = Х2 × У2 ) к индексам Х1 и У1.
Из пропорции:
Х2 / У1 = Х1 / У2
Получаем:
Х2 = Х1 × У1 / У2
Подставим в уравнение для S2:
S2 = Х2 × У2 = Х1 × У1 × У2 / У2 = Х1 × У1 = S1
В результате мы получили, что площадь куска с надписью "Витя" равна площади куска с надписью "Митя".