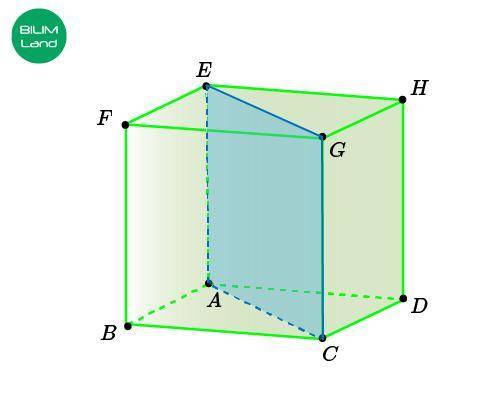
На чертеже дан куб ABCDEFGH, длина ребра которого равна 3 корень из 2
Найди расстояние от точки F до плоскости ACGE.
Другие вопросы по теме Геометрия
Популярные вопросы
- Відтворіть сюжет твору Р. Акутаґави: розташуйте події новели в логічному порядку....
3 - Відредагуйте речення з прямою мовою Дякую за моральну підтримку всміхнувся син....
2 - Look at the pictures and complete the dialoguesРешите продолжениє ...
1 - Выходили двенадцать месяцев, выносили пятьдесят два сокола, выпускали триста...
3 - В чому схожість і відмінність життя О.Олеся і М.Вороного?...
2 - 12. При рольовій ієрархії в угрупуванні бобрів тварини можуть виконувати функції...
2 - уравнение с двумя переменными при Х=2...
2 - 11 тапсырма Үлгі бойынша бір-біріңе қарсы жауап айтыңдар не бір-біріңді мақұлдаңдар...
3 - Знайдіть та випишіть антитези з новели павутинка ...
1 - Всем привет Help me pleaseНуєно найти 10% 20% 25% 50% от уравнения 27÷(x+6,4)=0,45...
2
Формула расстояния от точки до плоскости:
d = | Ax + By + Cz + D | / √(A^2 + B^2 + C^2)
где d - расстояние от точки до плоскости,
A, B, C - координаты вектора, нормального к плоскости,
D - коэффициент, определяющий положение плоскости.
Нам нужно найти расстояние от точки F до плоскости ACGE, поэтому сначала нам нужно найти координаты вектора, нормального к плоскости, и коэффициент D.
Плоскость ACGE образуется в результате пересечения граней ACG и AEG, поэтому воспользуемся координатами этих граней для определения нормали.
Координаты грани ACG: A(√2, 0, 0), C(3√2, 0, 0), G(3√2, 3√2, 0)
Координаты грани AEG: A(√2, 0, 0), E(√2, 0, 3√2), G(3√2, 3√2, 0)
Возьмем векторное произведение векторов AC и AG, чтобы найти нормальный вектор к плоскости ACGE.
Вектор AC: C - A = (3√2 - √2, 0 - 0, 0 - 0) = (2√2, 0, 0)
Вектор AG: G - A = (3√2 - √2, 3√2 - 0, 0 - 0) = (2√2, 3√2, 0)
Теперь выполним векторное произведение:
N = AC x AG = (2√2 × 3√2, 0 × 2√2 - 2√2 × 0, 2√2 × 3√2) = (12, 0, 12)
Теперь у нас есть нормальный вектор N(12, 0, 12) и координаты точки F(√2, √2, 3√2).
Заменим эти значения в формуле расстояния от точки до плоскости:
d = | (12)(√2) + (0)(√2) + (12)(3√2) + D | / √(12^2 + 0^2 + 12^2)
Для определения коэффициента D нам нужно использовать координаты одной из точек на плоскости. Мы можем взять, например, A.
Подставим координаты A(√2, 0, 0):
0 = (12)(√2)(√2) + (12)(3√2)(0) + D
0 = 48 + D
Теперь мы можем решить уравнение:
D = -48
Возвращаемся к формуле расстояния:
d = | (12)(√2) + (0)(√2) + (12)(3√2) - 48 | / √(12^2 + 0^2 + 12^2)
d = | 36√2 - 48 | / √(12^2 + 12^2)
d = | 36√2 - 48 | / √(144 + 144)
d = | 36√2 - 48 | / √(288)
d = | 36√2 - 48 | / 12√2
Чтобы упростить выражение, заметим, что 12√2 можно вынести за знак модуля:
d = | (√2)(36 - 48√2) | / 12√2
d = (36 - 48√2) / 12
d = 3 - 4√2
Таким образом, расстояние от точки F до плоскости ACGE составляет 3 - 4√2.