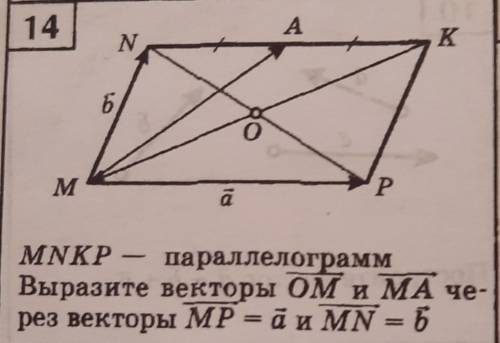
MNKP — параллелограмм Выразите векторы ОМ и МА через векторы MP = a и MN = b (нужно решение, ани ответ ) За не правильный ответ, или за шутку бан*

→МА=→МN+→NA=→b+→0.5a-по правилу треугольника; кроме того, т.к. →NK=→MP, →NA=→AK=0.5→NK=0.5→MP=0.5→а

→MK=→MN+→MP=→b+→a - по правилу параллелограмма

→OM=0.5→MK

-→OM=-0.5→MK

→0M=-→0.5b-→0.5a

Для того чтобы выразить векторы ОМ и МА через векторы MP = a и MN = b, нам необходимо использовать свойства параллелограмма.

Из свойств параллелограмма, мы знаем, что противоположные стороны параллелограмма равны по длине и параллельны. Значит, вектор МА равен вектору NP (так как NP – это противоположная сторона параллелограмма MNKP).

Теперь мы можем выразить вектор МА через векторы a и b следующим образом: МА = NP = -MN. Поскольку вектор b равен вектору MN, то: МА = -b.

Теперь нам осталось найти вектор ОМ.

Из свойств параллелограмма, мы также знаем, что диагонали параллелограмма делятся пополам. Значит, точка О – это середина отрезка МР.

Чтобы найти точку О, мы можем воспользоваться формулой середины отрезка:
О = (М + Р)/2.

Теперь мы можем выразить вектор ОМ следующим образом: ОМ = МО - МА.

Подставим выражения для О и МА:
ОМ = ((М + Р)/2) - (-b).

Раскроем скобки:
ОМ = (М + Р)/2 + b.

Таким образом, мы выразили векторы ОМ и МА через векторы a и b. Вектор МА равен -b, а вектор ОМ равен ((М + Р)/2) + b.

*Примечание: Принцип работы с параллелограммом применяется к решению данной задачи. Вектор МА может быть выражен как отрицательный вектор MN и вектор ОМ может быть найден как сумма половины суммы векторов MN и MP. Вектор ОМ также может быть найден как сумма вектора МР и вектора MN. В обоих случаях, решение будет давать тот же результат, как указано выше.