MNKP MNKP — параллелограмм. Его смежные стороны равны 40 см и 51 см, диагональ — 77см. Найди его площадь. Вырази ответ в см ^2 2

Ответы

AirinMandarin 05.02.2022 21:49

Пусть β - угол между смежными сторонами. По теореме косинусов:

77² = 40² + 51² - 2·40·51·cosβ ⇒ 2·40·51·cosβ = 40² + 51² - 77² ⇒

2·40·51·cosβ = 1600 + (51 - 77)·(51 + 77) = 1600 - 26·128 ⇒

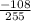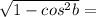
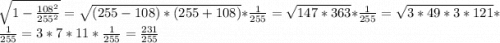
16·5·51·cosβ = 16·(100 - 26·8) ⇒ 5·51·cosβ = 100 - 26·8 = 100 - 208 = - 108 ⇒ cosβ = $\frac{-108}{255}$ , sinβ = $\sqrt{1 - cos^{2}b } =$ $\sqrt{1 - \frac{108^{2} }{255^{2} } } = \sqrt{(255-108)*(255+108)} * \frac{1}{255} = \sqrt{147*363} *\frac{1}{255} = \sqrt{3 * 49 * 3 *121} * \frac{1}{255} = 3* 7 * 11 *\frac{1}{255} = \frac{231}{255}$

⇒ площадь параллелограмма равна: S = 40 * 51 * sinβ =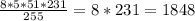 $\frac{8* 5* 51*231}{255} = 8* 231 = 1848$

ответ: площадь параллелограмма равна 1848 см²

ПОКАЗАТЬ ОТВЕТЫ

ivanovmax 15.01.2024 19:43

Для решения данной задачи нам необходимо использовать формулу для нахождения площади параллелограмма. Формула имеет вид: S = а * h, где S - площадь, а - длина основания, h - высота.

Итак, нам известны следующие данные:
- Смежные стороны параллелограмма равны 40 см и 51 см. Для удобства обозначим их как а и b, где а = 40 см, b = 51 см.
- Диагональ параллелограмма равна 77 см. Обозначим эту диагональ как d.

Теперь нам необходимо найти основание и высоту параллелограмма. Для этого воспользуемся теоремой Пифагора.

Согласно теореме Пифагора, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. В нашем случае, гипотенуза - это диагональ параллелограмма (d), а катеты - смежные стороны (а и b).

Таким образом, у нас есть следующая формула:
d^2 = a^2 + b^2.

Подставим известные значения:
77^2 = 40^2 + 51^2.

Теперь решим уравнение. Возведем значения в квадрат:
5929 = 1600 + 2601.
5929 = 4201.

Полученное равенство неверно, значит, мы сделали ошибку при подсчете. Рассмотрим другой подход.

Заметим, что параллелограмм MNKP можно разделить на два прямоугольных треугольника, используя диагонали MP и NK. Оба эти треугольника прилегают к основанию параллелограмма и имеют общую высоту (высоту параллелограмма).

Для нахождения площади каждого из этих треугольников нам понадобится использовать формулу S = (а * b) / 2, где а и b - это длины катетов.

Рассмотрим треугольник MNP. Основание этого треугольника равно 40 см, а высоту параллелограмма мы обозначим как h.

Тогда площадь этого треугольника будет равна:
S1 = (40 * h) / 2 = 20h.

Аналогично, рассмотрим треугольник NKP. Основание этого треугольника равно 51 см, а высоту параллелограмма также обозначим как h.

Площадь этого треугольника будет равна:
S2 = (51 * h) / 2 = 25.5h.

Объединяя оба треугольника, получим площадь параллелограмма:
S = S1 + S2 = 20h + 25.5h = 45.5h.

Осталось найти значение высоты h. Для этого воспользуемся теоремой Пифагора снова.

Мы уже знаем, что для треугольника MNP диагональ равна 77 см, а основание - 40 см. Тогда катет будет равен h.

Подставим значения в формулу Пифагора:
77^2 = длина катета^2 + 40^2.

Решим уравнение:
5929 = h^2 + 1600.
h^2 = 5929 - 1600 = 4329.

Извлечем квадратный корень:
h = √4329 ≈ 65.8.

Теперь, когда у нас есть значение высоты (h), мы можем найти площадь параллелограмма:
S = 45.5 * h = 45.5 * 65.8 ≈ 2996.9 см^2.

Итак, площадь параллелограмма MNKP равна примерно 2996.9 см^2.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия