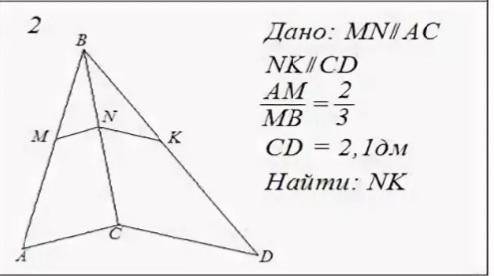
MN паралельно AC, NK параллельно CD AM/MB=2/3 CD=2.1 см найти: NK

Для решения данной задачи, мы можем использовать свойства параллельных прямых и пропорции.

Обратим внимание, что в задаче дано, что MN параллельно AC и NK параллельно CD. Это означает, что у нас есть две пары параллельных прямых: MN и AC, NK и CD.

Дано также, что AM/MB = 2/3 и CD = 2.1 см.

1. Для начала, посмотрим на отношение AM/MB. В задаче сказано, что AM/MB = 2/3. Это означает, что отрезок AM составляет 2 части от общей длины отрезка AB, а отрезок MB - 3 части. Мы можем записать это отношение в виде AM/AB = 2/5, так как AM + MB = AB.

2. Зная, что MN параллельно AC, мы можем использовать свойство параллельных прямых, которое гласит, что отрезки, проведенные параллельно одной стороне, делят каждые две параллельных стороны пропорционально. В нашем случае, это означает, что отрезок MN делит отрезки AB и AC пропорционально.

3. Из первого шага мы знаем, что AM/AB = 2/5. Если мы применяем свойство параллельных прямых, то AM/AB = NK/CD. Таким образом, мы можем записать это в виде NK/CD = 2/5.

4. Заменяем значение CD на 2.1 см в уравнении: NK/2.1 = 2/5.

5. Теперь нам нужно найти значение NK. Чтобы найти значение неизвестной, мы можем кросс-умножить значения по обеим сторонам уравнения. Таким образом, мы получаем: NK = (2/5) * 2.1.

6. Подсчитываем это значение: NK = 0.84 см.

Таким образом, ответ на задачу составляет NK = 0.84 см.