меня эта геометрия до истерики доведет
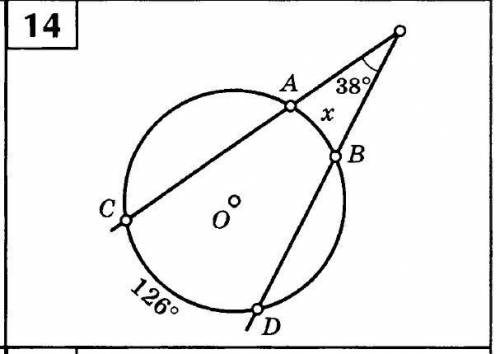
Нужно найти x

Для решения этой задачи, нам необходимо использовать свойство радиуса, содержащего хорду, которое гласит: радиус перпендикулярен хорде в точке пересечения радиуса и хорды.

Данная геометрическая фигура представляет собой окружность, в которой имеется хорда AB и радиус OC, пересекающий хорду AB в точке D.

Мы можем обозначить точку пересечения этих двух линий как D. Важно заметить, что OD - это радиус окружности, который по определению равен 8 см.

Теперь мы можем приступить к решению задачи. Воспользуемся теоремой о прямоугольных треугольниках.

В треугольнике OCD, угол COD прямой (так как радиус перпендикулярен хорде), поэтому треугольник OCD является прямоугольным.

Мы знаем, что OD равен 8 см, а CD равен половине AB (по свойству хорды, которое утверждает, что хорда делит радиус пополам).

Теперь давайте обратимся к самому треугольнику OCD. Зная значение OD (8 см) и CD, мы можем использовать теорему Пифагора, которая гласит: квадрат гипотенузы (OD) равен сумме квадратов катетов (CD и OC).

Таким образом, мы можем записать уравнение в следующем виде:
OD^2 = CD^2 + OC^2

Подставляя известные значения, получим:
8^2 = (AB/2)^2 + OC^2

Разрешив это уравнение относительно AB (или хорды), мы найдем значение х путем подставления известных значений в уравнение.

Важно отметить, что знак квадратного корня может быть как положительным, так и отрицательным, и в данном случае мы должны выбрать положительное значение, так как размер AB не может быть отрицательным.

Итак, получается:
8^2 - OC^2 = (AB/2)^2

64 - OC^2 = (AB/2)^2

Подставляя значение OC^2 (известное из изначального изображения окружности) и решая это уравнение, мы найдем значение х.

Надеюсь, это решение поможет вам понять и решить данную задачу по геометрии.