Медиана равностороннего треугольника равна 12 корней из 3. найдите его сторону.

Дан равносторонний ΔABC. Медиана BM=12√3.

Найти сторону ΔABC.

В правильном треугольника медиана является и высотой, откуда BM⊥AC.

Углы между сторонами правильного треугольника равны по 60°, поэтому ∠BCA=60°.

В прямоугольном ΔВМС (∠М=90°): BM=12√3, ∠BCM=60°;

синус острого угла в прямоугольном треугольнике это отношение противолежащего катета к гипотенузе, откуда

sin∠BCM = BM/BC ⇒ BC=BM/(sin∠BCM)

BC=(12√3)/(sin60°)=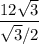 = 12·2=24

ответ: 24.