Медіани BF і CN трикутника АВС дорівнює 27 см і 36 см відповідно,а кут між ними дорівнює 90градусів.Знайдіть медіану АР.
Другие вопросы по теме Геометрия
Популярные вопросы
- Анализ скульптуры медный всадник (необязательно именно его)по плану: 1автор,...
1 - Глава вторая произведения мертвые души . (помещик - манилов) 1. фио помещика...
2 - Дан следующий вариационный ряд 1 2 3 4 5 6 7 8 9 10 1 1 2 2 4 4 4 5 5 5 требуется...
3 - Бджола летить зі швидкістю 6м/с.за який час бджола долетить до вулика, якщо...
3 - Выпишите предложения с обособленными и.определите чем выражено обособленные...
1 - Сравнительная характеристика степей из произведения и.с тергенева лес и степь...
1 - 3a) read again. who are thepeople in the pictures (1-6)? explain the words...
3 - Мне надо объяснить особенности новой культуры на примере из 29 параграфа...
1 - Роль однотематической лексики как средства связи между предложениями? ...
3 - Log0,8 5*log5 1,25 найти значение выражения...
3
Всі три медіани перетинаються в одній точці і точкою перетину медіан трикутника кожна медіана ділиться у відношенні 2:1, рахуючи від вершини трикутника. Значить,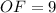 см і
см і 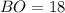 см;
см; 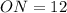 см і
см і 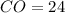 см.
см.
З прямокутного трикутника FOC:
З прямокутного трикутника COB:
З прямокутного трикутника NOB:
Оскільки, BF, AP, CN - медіани, то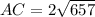 см і
см і 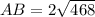 см.
см.
Добудуємо трикутник ABC до паралелограма ABDC. Сума квадратів діагоналей паралелограма дорівнює сумі його всіх сторін.
Відповідь: 45 см.