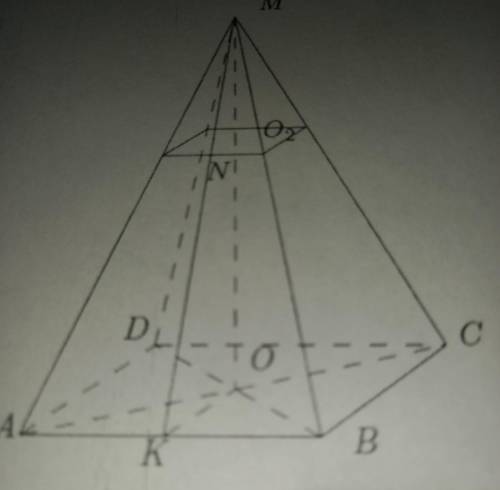
MABCD Правильная пирамида
A1B1C1 || ABC
MO2:OO2= 1:2
NK- апофема
NK=4 см
Sкрив.пир.полн= 186 см^2
найти: ОО2

Для решения этой задачи нам понадобится использовать два важных свойства правильной пирамиды.

1. В правильной пирамиде любое поперечное сечение, параллельное основанию, является подобным основанию. То есть, если мы возьмем какое-либо поперечное сечение пирамиды, оно будет подобно ее основанию.

2. Отношение объемов двух правильных пирамид с одинаковыми высотами равно отношению кубов их апофем. Если мы возьмем две правильные пирамиды с одинаковыми высотами, отношение объемов этих пирамид будет равно отношению кубов их апофем.

Теперь перейдем к решению задачи.

Задача: Найти длину отрезка ОО2.

Дано:
- MABCD - правильная пирамида,
- A1B1C1 || ABC (основание пирамиды и верхняя часть пирамиды параллельны),
- MO2:OO2= 1:2 (отношение расстояний от вершины пирамиды M до точек O2 и О равно 1:2),
- NK - апофема пирамиды,
- NK = 4 см (длина апофемы),
- Sкрив.пир.полн = 186 см^2 (площадь поверхности полной пирамиды).

Решение:
1. Используя свойство поперечного сечения параллельного основанию пирамиды, мы можем сделать вывод, что поперечное сечение пирамиды, проходящее через точку O2, будет подобно основанию ABC.

2. Поскольку пирамида MABCD правильная, поперечное сечение, проходящее через точку O2, будет правильным треугольником. Поэтому отрезок O2N будет проведен через середину стороны AB (поскольку O2M:MO2= 1:2).

3. Зная, что поперечное сечение, проходящее через точку O2, подобно основанию ABC, и высота пирамиды равна отрезку NK, мы можем записать соотношение:
Sкрив.пир.полн / Sоснов.пир.вед = (OO2 / NK)^2,

где Sоснов.пир.вед - площадь основания введенной пирамиды.

Поскольку пирамида MABCD правильная, площадь основания введенной пирамиды равна площади основания полной пирамиды, поэтому мы можем записать:
Sкрив.пир.полн / Sоснов.пир.общ = (OO2 / NK)^2,

где Sоснов.пир.общ - площадь основания полной пирамиды.

4. Подставляем известные значения и решаем уравнение:

186 / Sоснов.пир.общ = (OO2 / 4)^2.

5. Решаем получившееся уравнение относительно OO2:

OO2^2 = 4^2 * (186 / Sоснов.пир.общ).

6. Находим квадратный корень из обеих сторон уравнения:

OO2 = 4 * sqrt(186 / Sоснов.пир.общ).

Таким образом, длина отрезка ОО2 равна 4 * sqrt(186 / Sоснов.пир.общ).