M(-4; 3) l(-1; -5) n(4; 0) а)определите вид треугольника б) найдите координаты серединых сторон в) найдите длину спедней линии паралельной основарию г) найдите площадь треугольника
Другие вопросы по теме Геометрия
Популярные вопросы
- с химией ( ) Задание на картинке:...
2 - Реймсский собор характеристика (внешний вид)...
2 - Перед вертикально поставленным плоским зеркалом стоит человек. Как изменится...
1 - Знайди множину цілих розв язків нерівностей, зроби малюнок 1.|x| 42.|x+4|≥73.|x|...
1 - Үлкендердің көмегімен Толағай тауы туралы деректі ізде. Тау еліміздің қай...
2 - В чём отличие между кораблями? Как называется здание на вершине холма? Из...
1 - Установите соответствие между крайними точками Австралии и их названиями....
2 - висновок на тему визначення густин твердого тила та ридини...
2 - , напишите краткий пересказ, того, что покажу (на русском) со страницы 8-11...
3 - Решите 2-4 номер по английскому !...
2
а)
Равнобедренный (основание LN), остроугольный
б)
Середина ML: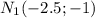
Середина MN: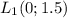
Середина LN: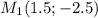
в)
г)
Объяснение:
а)
Найдем длины сторон:
Отсюда треугольник равнобедренный, а также из того, что боковые стороны больше основания, остроугольный.
б)
Середина ML: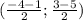 , то есть
, то есть 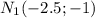
Середина MN: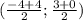 , то есть
, то есть 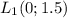
Середина LN: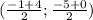 , то есть
, то есть 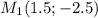
в)
Длина средней линии, параллельной основанию, равна половине длины основания, то есть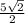
г)