лучше бы конечно до утра ;) за ранее тем кто спамит, жалобу

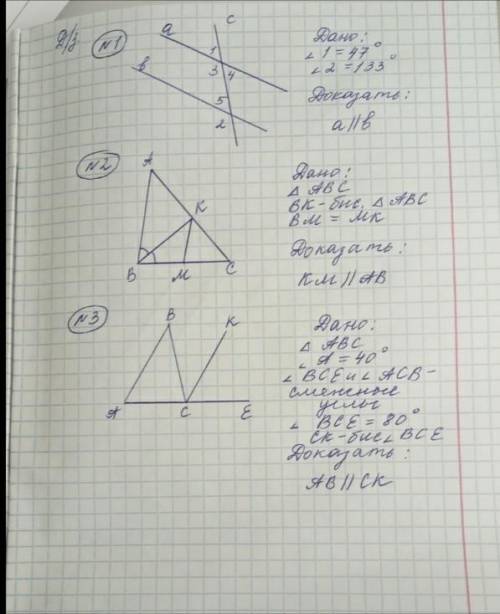
№1

Углы 2 и 5 смежные, их сумма равна 180°. Значит, ∠5=180-133=47°.

Углы 1 и 5 соответственные при прямых a и b и секущей c, ∠1=47° и ∠5=47°, ⇒ a||b (по признаку параллельных прямых: если соответственные углы равны, то прямые параллельны) ч.т.д.

№2

Так как по условию  BM=MK, то △BMK - равнобедренный. В равнобедренном треугольнике углы при основании равны, значит ∠KBM=∠BKM.

Так как по условию BK - биссектриса △ABC, то ∠ABK=∠KBC=∠KBM.

Итак, ∠KBM=∠BKM и ∠ABK=∠KBM.  Значит, ∠ABK=∠BKM, при этом ∠ABK и ∠BKM -  внутренние накрест лежащие углы при прямых AB и KM и секущей BK, ⇒ KM||AB,  (по признаку параллельных прямых: если внутренние накрест лежащие углы равны, то прямые параллельны) ч.т.д.

№3

Так как по условию ∠BCE=80° и CK - биссектриса ∠BCE, то ∠KCE=∠BCE:2=80°:2=40°.

∠BAC=40° (по условию) и ∠KCE=40°, при этом ∠BAC и ∠KCE -  соответственные углы при прямых AB и СK и секущей AE, ⇒ AB || СK (по признаку параллельных прямых: если соответственные углы равны, то прямые параллельны) ч.т.д. .