Куля, радіус якої дорівнює 5 см, дотикається до всіх сторін трикутника зі сторонами 15 см, 15 см і 24 см. Знайдіть відстань від центра кулі до площини трикутника.
Другие вопросы по теме Геометрия
Популярные вопросы
- Напишите, , сочинение на тему: моя хата с краю - ничего не знаю...
1 - Составить диалог по яз на тему: экологическая ситуация в украине...
2 - Вопрос, которого нигде нет. , кто знает, : на какие две группы...
1 - Какие связи имеются в молекуле оксида серы?...
1 - Почему нельзя приливать воду в серную кислоту? ?...
3 - Прислів я і прикмети прислів я і прикмети про дощ,град,сніг,іній...
2 - Вправильный шестиугольник со стороной a вписана окружность. найдите...
3 - Могут ли две различные плоскости иметь только одну общую точку?...
2 - Напишите когда началась и закончилась блокада ленинграда !...
2 - Опишите передвижения одноклеточных организмов....
3
Объяснение:
Щоб знайти відстань від центра кулі до площини трикутника, ми можемо використати теорему Піфагора. Теорема Піфагора говорить, що в прямокутному трикутнику квадрат гіпотенузи рівний сумі квадратів катетів. В нашому випадку, ми знаємо, що радіус кулі складає 5 сантиметрів, і це буде наша гіпотенуза. Також ми знаємо, що сторони трикутника складають 15 сантиметрів і 15 сантиметрів, і це будуть наші катети. Тепер ми можемо розв'язати рівняння, щоб знайти відстань від центра кулі до площини трикутника:
h^2 = 5^2 - (15^2 + 15^2) / 2
h^2 = 25 - 225
h^2 = -200
h =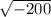
На жаль, коренем з від'ємного числа не може бути, тому ми можемо сказати, що куля не може дотикатися до всіх сторін трикутника. Щоб куля могла дотикатися до всіх сторін трикутника, радіус кулі повинен бути більшим ніж піввисота трикутника.