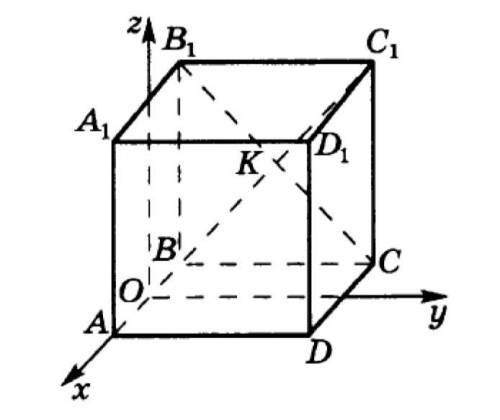
Куб ABCDA1B1C1D1 помещён в прямоугольную систему координат (см. рисунок), O – середина ребра AB, С(-2;4;0). а) Найдите координаты всех остальных вершин куба.
б) Найдите координаты векторов OC, OB1 и OK и разложите их по координатным векторам i, j и k.
Другие вопросы по теме Геометрия
Популярные вопросы
- Який тиск чинить газ за температури 27 •с у посудині місткістю 2л,...
2 - Вычислите, на сколько процентов отличается длинна окружности найденная...
3 - Произведение в дурном обществе какое было отношение васи к отцу...
3 - Что из перечисленного ниже не является формой рельефа, образованной...
1 - Какие одинаковые качества ,есть у чичикова и его помещиков ?...
2 - Решите уравнение: (3+4x)(9-12x+16x^2)-16x(4x^2-1)= -5...
1 - Смешали два раствора один из которых содержит 24 г...
3 - 1) решить : пловец нырял 4 раза и каждый раз доставал со дна по...
1 - Сделать изложение по рассказу петька на даче. со слов в первые два...
1 - Внешняя политика петра 3. только надо по событиям и с датами. (основные,...
2
Дано:
ABCDA₁B₁C₁D₁ - куб
O – середина ребра AB
С(-2;4;0)
Найти:
а) Найдите координаты всех остальных вершин куба.
б) Найдите координаты векторов OC, OB₁ и OK
а) A(2,0,0); B(-2,0,0); D(2,4,0); A₁(2,0,4); B₁(-2,0,4); C₁(-2,4,4); D₁(2,4,4)
б) вектор OC (-2,4,0) ⇒ вектор OC = -2i+4j+0k
вектор OB₁ (-2,0,4) ⇒ вектор OB₁ = -2i+0j+4k
вектор OK (-2,2,2) ⇒ вектор OK = -2i+2j+2k
(K - середина BC₁ и B₁C ⇒ k(-2,2,2))
ответ: а) A(2,0,0); B(-2,0,0); D(2,4,0); A₁(2,0,4); B₁(-2,0,4); C₁(-2,4,4); D₁(2,4,4)
б) вектор OC = -2i+4j+0k, вектор OB₁ = -2i+0j+4k, вектор OK = -2i+2j+2k