КТО ШАРИТ ПО ГЕОМЕТРИИ? 1.Стороны треугольника равны 29 см, 25 см, 6 см.
Вычисли наибольшую высоту этого треугольника.
Наибольшая высота равна__см.
Дополнительные вопросы:
a. какие формулы площади треугольника используются в решении задачи?(выбрать несколько)
(картинка снизу)
b. Чему равна площадь треугольника? __см².
c. Какое высказывание верное?
1-В треугольнике наибольшая та высота, которая проведена к наибольшей стороне
2-В треугольнике наибольшая та высота, которая проведена к наименьшей стороне
2.В треугольнике стороны равны 17см, 25см и 28см. Вычислите радиус окружности, вписанной в этот треугольник.
В ответ запишите только число. Если необходимо, ответ округлите до целого числа.
3.В треугольнике KTP сторона KT=5см, углы ∠K=30°; ∠P=80°. Определите площадь треугольника.
В ответ запишите только число. Если необходимо, ответ округлите до целого числа. Промежуточные результаты вычислений округляйте до тысячных.
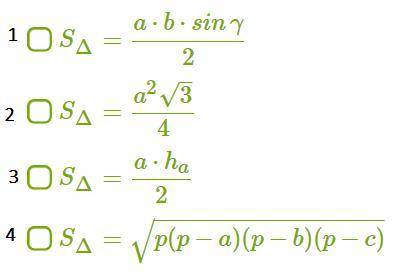
Другие вопросы по теме Геометрия
Популярные вопросы
- Средний рост 15 учеников в классе равен 140 см. после того, как один...
1 - Кроссворд по обж наводнение придумайте 35 слов. с интренета !...
1 - Нужна сравнительная характеристика круглых и кольчатых червей...
1 - Площадь садового участка - 6 соток. огурцами занято 3/8 площади участка....
3 - 1) через лампу накаливания проходит ток 0.8 ампер сколько электронов...
3 - Решить по , а) стиральная машина стоит 9384 р., включая доставку на...
1 - Для получения окрашенных луковиц необходимо наличие у растений лука...
3 - Найдите среднее арифметическое: 3,234; 3,452; 4,185; 2,892 и округлите...
3 - Впрямоугольном треугольнике abc угол b=90, гипотенуза ab=55, cosb=0,8...
2 - Полихлорвинил слипается лучше, чем полиэтилен. почему?...
3
1. Для того чтобы найти наибольшую высоту треугольника, нам нужно знать его стороны. В данном случае, стороны треугольника равны 29 см, 25 см и 6 см.
Для начала, найдем самую длинную сторону треугольника. В данном случае, это сторона длиной 29 см.
Теперь мы можем использовать формулу для нахождения высоты треугольника, которая проведена к наибольшей стороне:
Высота = (2 * Площадь треугольника) / Сторона треугольника
Перед тем, как мы сможем использовать эту формулу, нам нужно найти площадь треугольника.
a. Площадь треугольника можно найти, используя несколько формул на выбор.
Одна из формул, которую можно использовать, - это формула Герона:
Площадь = √(p * (p - a) * (p - b) * (p - c))
Где p - полупериметр треугольника (p = (a + b + c)/2), а a, b и c - стороны треугольника.
Другой формулой, которую можно использовать, - это формула для прямоугольного треугольника:
Площадь = (a * b) / 2
Где a и b - катеты прямоугольного треугольника.
В данной задаче, нам не дано информации, что треугольник прямоугольный, поэтому мы будем использовать формулу Герона для нахождения площади треугольника.
Подставим значения сторон треугольника в формулу Герона:
Полупериметр треугольника, p = (29 + 25 + 6) / 2 = 60 / 2 = 30 см
Площадь = √(30 * (30 - 29) * (30 - 25) * (30 - 6))
= √(30 * 1 * 5 * 24)
= √(3600)
= 60 см²
b. Теперь, когда мы нашли площадь треугольника, мы можем использовать формулу для высоты треугольника:
Высота = (2 * 60 см²) / 29 см
Высота ≈ 4.138 см (округляем до тысячных)
Таким образом, наибольшая высота этого треугольника составляет около 4.138 см.
c. Следующий вопрос - какое из высказываний верно относительно наибольшей высоты треугольника?
1-В треугольнике наибольшая та высота, которая проведена к наибольшей стороне
2-В треугольнике наибольшая та высота, которая проведена к наименьшей стороне
Верное высказывание - 1. В треугольнике наибольшая та высота, которая проведена к наибольшей стороне.
2. Вторая задача:
В треугольнике стороны равны 17 см, 25 см и 28 см.
Мы должны найти радиус окружности, которая вписана в этот треугольник.
Нам известно следующее:
Радиус вписанной окружности треугольника равен полупериметру треугольника, разделенному на его полупериметр:
Радиус = (a + b + c) / (2 * p)
Где a, b и c - стороны треугольника, а p - его полупериметр.
Подставим значения сторон треугольника в эту формулу:
Радиус = (17 + 25 + 28) / (2 * (17 + 25 + 28) / 2)
= (70) / (70)
= 1
Таким образом, радиус окружности, вписанной в данный треугольник, равен 1.
3. Третья задача:
В треугольнике KTP известно, что сторона KT = 5 см, а углы ∠K = 30° и ∠P = 80°.
Необходимо найти площадь этого треугольника.
Для нахождения площади треугольника при известной стороне и двух углах, мы можем использовать следующую формулу:
Площадь = (1/2) * a * b * sin(γ)
Где a и b - стороны треугольника, а γ - угол между ними.
Подставим известные значения в формулу:
Площадь = (1/2) * 5 см * 5 см * sin(80°)
≈ 12.043 см² (округляем до тысячных)
Таким образом, площадь треугольника KT = 12 см² (округляем до целого числа).
Надеюсь, это решение помогло тебе в понимании задачи и использовании формул геометрии. Если у тебя есть еще вопросы, не стесняйся задавать! Я всегда готов помочь!