;--; кончились (

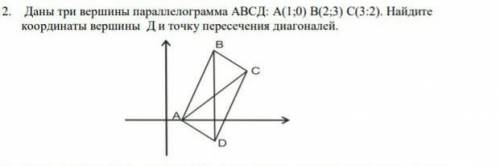
Даны три вершины параллелограмма АВСД: А(1;0) В(2;3) С(3:2). Найдите

координаты вершины Д и точку пересечения диагоналей.​

Для решения данной задачи мы можем воспользоваться свойствами параллелограмма.

1. Найдем координаты вершины Д:
- Мы знаем, что в параллелограмме противоположные стороны равны и параллельны. Из этого следует, что сторона АВ параллельна стороне СД и сторона ВС параллельна стороне АД.
- Координаты вершины Д будут равны координатам точки В (2;3) сдвинутым на вектор (вектор АС = С - А = (3-1;2-0) = (2;2)).
- Значит, координаты вершины Д будут равны (2;3) + (2;2) = (4;5).

2. Найдем точку пересечения диагоналей:
- В параллелограмме, диагонали делятся пополам и их пересечение является точкой медианы.
- Найдем середину диагонали АС, которая соединяет вершины А и С. Координаты середины можно найти, как среднее арифметическое координат концов диагонали, т.е. (xСеред, yСеред) = ((xА + xС) / 2, (yА + yС) / 2).
- Подставляем координаты вершин А(1;0) и С(3;2) в формулу: (xСеред, yСеред) = ((1+3) / 2, (0+2) / 2) = (2, 1).
- Значит, точка пересечения диагоналей будет иметь координаты (2, 1).

Таким образом, координаты вершины Д равны (4, 5), а точка пересечения диагоналей имеет координаты (2, 1).