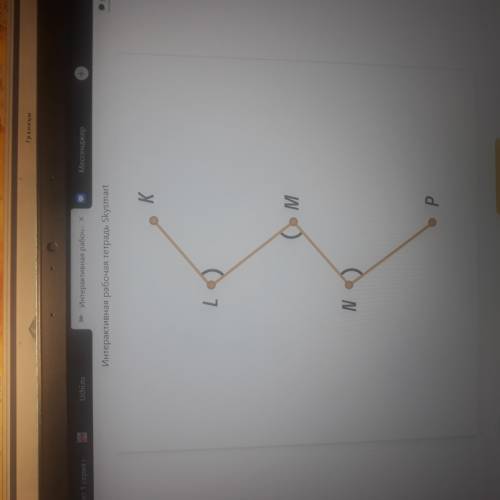
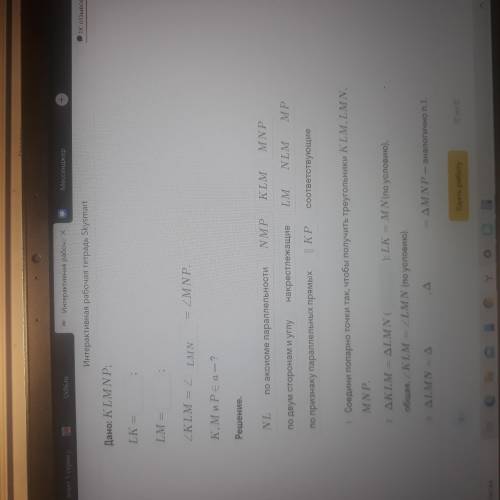
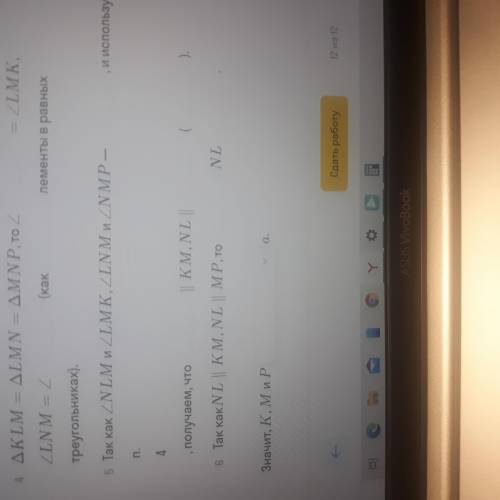
КLMNP состоит из равных отрезков LK и MN, LM и NP, которые образуют равные углы КLM, LMN, MNP. Определите, принадлежат ли точки K, M и P одной прямой а и если да, то почему?
Другие вопросы по теме Геометрия
Популярные вопросы
- В деревне, (1) где родился Михаил Васильевич Ломоносов, (2)не осталось...
3 - 1. Яке видання творів Т. Шевченка було надруковане з присвятою Марку Вовчку?...
2 - Подготовьте сообщение о природных сообществах родного края(г.Пенза). Найдите...
1 - (т+0,1)*1,5=17,004 чему равеен т...
1 - Прочтите фрагмент исторического источника и выполните задания 19, 20. Используйте...
1 - Укажить рядок у якому всі НЕ є знаменниками А. Їхній, самий , такий В....
1 - trainers are these?1.whose 2.why. 3.when.4 who ...
3 - Як ви розумієте вислів з казки притчі автора А. де Сент-Екзюпері: Люди...
1 - Люди Совсем не шарб в графиках...
3 - Вкажіть назву держави, яка зображена на карті: Китай, Греція, Рим...
1
Итак, у нас есть треугольник KLM с углом КLM, треугольник LMN с углом LMN, и треугольник MNP с углом MNP. Мы знаем, что эти углы равны между собой, поэтому мы можем сказать, что:
угол КLM = угол LMN = угол MNP
Используя теорему о сумме углов треугольника, мы можем записать:
(угол КLM) + (угол LMN) + (угол MNP) = 180 градусов
Так как углы равны между собой, мы можем записать:
x + x + x = 180 градусов
где x - мера каждого угла (то есть, каждый угол равен x градусам).
Решим эту уравнение для x:
3x = 180 градусов
x = 180 градусов / 3
x = 60 градусов
Таким образом, каждый угол (угол КLM, угол LMN и угол MNP) равен 60 градусам.
Теперь обратимся к треугольнику KMP. Мы можем написать, что:
(угол КLM) + (угол LMN) + (угол MNP) + (угол KMP) = 180 градусов
Подставим известные значения:
60 градусов + 60 градусов + 60 градусов + (угол KMP) = 180 градусов
180 градусов + (угол KMP) = 180 градусов
(угол KMP) = 0 градусов
Очевидно, что угол KMP равен 0 градусов, что означает, что отрезки KM и MP лежат на одной прямой.
Таким образом, точки K, M и P лежат на одной прямой, что подтверждает, что они принадлежат прямой а.