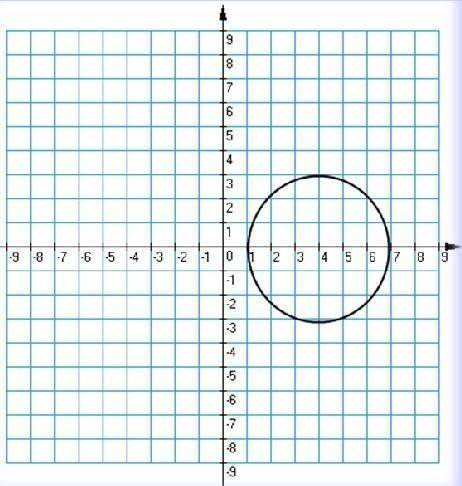
Какому уравнению окружности соответствует рисунок?

Чтобы определить уравнение окружности, соответствующей данному рисунку, нам нужно использовать информацию о центре и радиусе окружности.

На изображении мы видим, что центр окружности находится в точке (2, -3). Это означает, что координаты центра окружности равны (2, -3).

Также на рисунке у нас есть точка на окружности, обозначенная как (5, 0). Мы можем использовать эту информацию для определения радиуса окружности.

Радиус окружности — это расстояние от центра окружности до любой точки на ней. Мы можем использовать формулу для расстояния между двумя точками в координатной плоскости:

d = √((x₂ - x₁)² + (y₂ - y₁)²),

где (x₁, y₁) и (x₂, y₂) - координаты двух точек.

Применяя эту формулу к точкам (2, -3) и (5, 0), мы получим:

d = √((5 - 2)² + (0 - (-3))²),
= √(3² + 3²),
= √(9 + 9),
= √18.

Теперь мы знаем, что радиус окружности равен √18.

Таким образом, уравнение окружности можно записать в виде:

(x - h)² + (y - k)² = r²,

где (h, k) - координаты центра окружности, и r - радиус окружности.

Подставляя известные значения, мы получаем:

(x - 2)² + (y - (-3))² = (√18)²,
(x - 2)² + (y + 3)² = 18,
(x - 2)² + (y + 3)² = 18.

Таким образом, уравнению окружности на данном рисунке соответствует выражение (x - 2)² + (y + 3)² = 18.