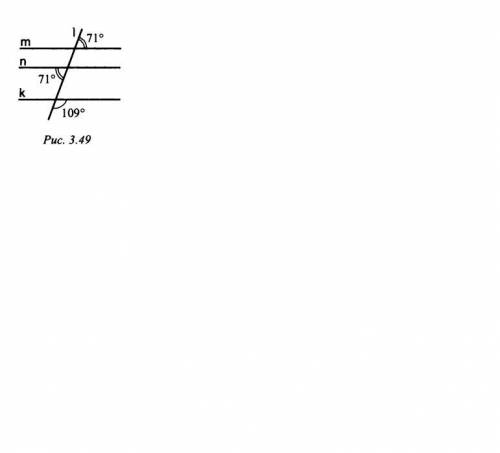
Какие из прямых m, n, k, изображенны на рисунке,являются параллельными?

На рисунке изображены три прямые: m, n и k. Для определения, какие из них являются параллельными, мы можем использовать следующий признак.

Прямые m и k называются параллельными, если и только если они имеют одинаковый угловой коэффициент. Угловой коэффициент для наклонной прямой можно получить, вычислив отношение изменения по оси y к изменению по оси x между двумя точками на прямой.

Давайте посмотрим на прямые m, n и k на рисунке и найдем их угловые коэффициенты.

Прямая m проходит через точки (1, 2) и (3, 6). Изменим первую точку на (0, 0), чтобы упростить вычисления. Изменилось только начало координатной системы, а угловой коэффициент прямой останется тем же.

Изменение по оси y равно:
6 - 2 = 4

Изменение по оси x равно:
3 - 1 = 2

Таким образом, угловой коэффициент прямой m равен 4/2 = 2.

Прямая n проходит через точки (0, 3) и (4, 9).

Изменение по оси y равно:
9 - 3 = 6

Изменение по оси x равно:
4 - 0 = 4

Таким образом, угловой коэффициент прямой n равен 6/4 = 3/2.

Прямая k проходит через точки (0, 1) и (3, 3).

Изменение по оси y равно:
3 - 1 = 2

Изменение по оси x равно:
3 - 0 = 3

Таким образом, угловой коэффициент прямой k равен 2/3.

Теперь, чтобы определить, какие прямые параллельны, сравним их угловые коэффициенты.

У прямых m и k угловые коэффициенты равны 2 и 2/3 соответственно. Они не являются равными. Следовательно, прямые m и k не являются параллельными.

У прямых m и n угловые коэффициенты равны 2 и 3/2 соответственно. Они также не являются равными. Значит, прямые m и n не параллельны.

Наконец, у прямых n и k угловые коэффициенты равны 3/2 и 2/3 соответственно. Они также не равны. То есть, прямые n и k не параллельны друг другу.

Таким образом, на рисунке все три прямые m, n и k не являются параллельными друг другу.