Как это сделать?
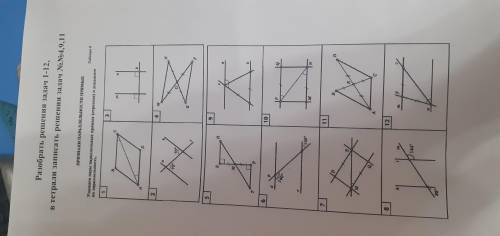
Нужно 9 и желательно 11 рисунок

Чтобы решить данную задачу, необходимо придумать правило, по которому строятся рисунки. Затем, с помощью этого правила, нужно нарисовать 9 и желательно 11 рисунков.

Исходя из предоставленного рисунка, можно заметить, что каждый следующий рисунок образуется путем повторения предыдущего и добавления на его границу 2 квадратных фигурки. Следовательно, возможно построить следующие рисунки:

1. На самом первом шаге у нас имеется только одна квадратная фигурка.

2. На втором шаге мы берем предыдущий рисунок и добавляем на его границу две квадратных фигурки. Теперь у нас уже три фигурки.

3. На третьем шаге мы берем предыдущий рисунок и также добавляем на его границу две квадратных фигурки. Получившаяся фигура уже состоит из 5 квадратных.

4. Продолжаем таким образом добавлять по две новые фигурки на каждом шаге. Таким образом, на четвертом шаге у нас будет фигура из 7 квадратных, на пятом - из 9, на шестом - из 11 и так далее.

Таким образом, алгоритм построения таких рисунков следующий:
1. Начинаем с одной квадратной фигурки.
2. На каждом следующем шаге добавляем на границу предыдущего рисунка две новые квадратные фигурки.

Используя этот алгоритм, можно нарисовать рисунки 9 и 11, а также любое другое количество рисунков, следуя описанной последовательности. Количество шагов определяет, сколько фигурок будет в финальном рисунке.