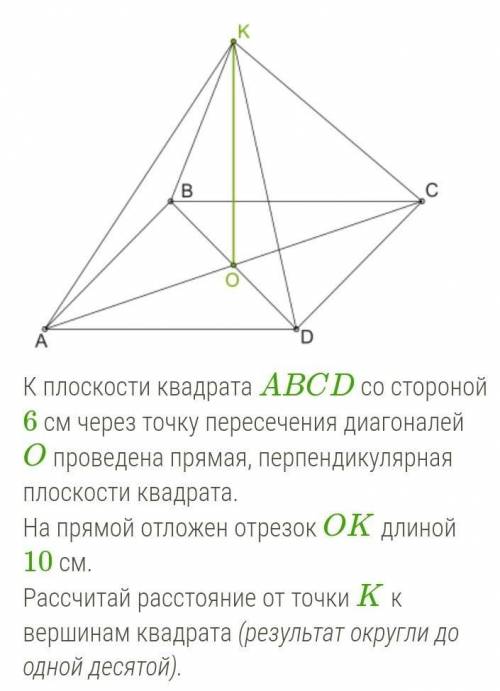
К плоскости квадрата ABCD со стороной 6 см через точку пересечения диагоналей O проведена прямая, перпендикулярная плоскости квадрата. На прямой отложен отрезок OK длиной 10 см.
Рассчитай расстояние от точки K к вершинам квадрата
Другие вопросы по теме Геометрия
Популярные вопросы
- Найдите значение выражений: 1) 3/5 - 1/7 2) 9/17 - 19/68 3) 4/15 - 11/60...
2 - Какое место службы занимает пётр гринёв и швабрин в повести ,, капитанская дочка...
3 - Вчем особеность строения глазь у рыб...
2 - В5 банок разлили поровну 25 л краски ,сколько литров краски понадобится ,что...
2 - Найдите значение выражения 2√2*5√3*3√10...
3 - Образец сочинения на тему новогодние хлопоты для 4 класса...
2 - Воротись, поклонись глаголы какого времени...
3 - Из 2-ух предложений выберете причастия и напишите морфологический разбор причастия(по...
3 - Среди двузначных простых чисел, разные разными цифрами есть такие короткие статусы...
1 - Скорость легкогого авто мобиля а км.ч,он проехал 5 км/час,сколько времени пробыл...
2
По условию, у нас есть квадрат ABCD со стороной 6 см. Определим вершины квадрата:
A – верхняя левая вершина
B – верхняя правая вершина
C – нижняя правая вершина
D – нижняя левая вершина
Также нам дано, что через точку пересечения диагоналей O проведена прямая, перпендикулярная плоскости квадрата. Обозначим точку пересечения диагоналей как O. Таким образом, наша задача – найти расстояние от точки K до вершин квадрата.
Для начала построим перпендикулярную прямую к плоскости квадрата ABCD, проходящую через точку O. Обозначим точку пересечения этой прямой с плоскостью квадрата как K.
Теперь у нас есть прямоугольный треугольник OKD, где OK – отрезок длиной 10 см, OD – сторона квадрата, то есть 6 см.
Чтобы найти расстояние от точки K до вершин квадрата, нам нужно разделить отрезок OK пополам и отложить его от точки K в направлении, противоположном стороне квадрата.
1. Построим перпендикулярную прямую от точки O к стороне CD квадрата. Обозначим точку пересечения этой прямой с CD как M. Поскольку прямая OM перпендикулярна стороне квадрата, и OM является своим половинным диагональным отрезком, то OM = OD/2 = 6/2 = 3 см.
2. Перейдем к треугольнику OKM. Мы знаем, что отрезок MK равен половине отрезка OK (так как M находится на половине OK) – MK = OK/2 = 10/2 = 5 см.
3. Теперь у нас есть треугольник KMD, где DM = MK = 5 см, и KD = DM - OM = 5 - 3 = 2 см. По теореме Пифагора, в прямоугольном треугольнике KMD можем найти значение KM (растояние от K до вершины D):
KM = √(KD^2 + DM^2)
KM = √(2^2 + 5^2)
KM = √(4 + 25)
KM = √29
KM ≈ 5.39 см.
Таким образом, расстояние от точки K до вершин квадрата примерно равно 5.39 см.