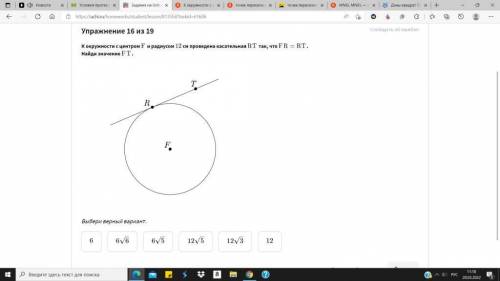
К окружности с центром F и радиусом 12 см проведена касательная RT так, что FR = RT. Найди значение FT .
Другие вопросы по теме Геометрия
Популярные вопросы
- Содной стороны сада,которую освещала луна,смутно липы зеленели. которую...
1 - Напишите мини сочинение 4 классу на тему как я провел весенние каникулы...
1 - Найдите естественную область определения: 7 x-1/x(x-5)...
2 - Составить речь для войска от имени александра македонского перед боем. 30...
2 - Построить треуголник по стороне и двум прилежащем к ней углам. решите єту...
1 - Вмагазине скидка на все товары 10%. старая цена фена - 2000 рублей. какова...
2 - д) 3/14•7/12-3/14•1/12 е) x: 5/4=24/35 ж) 7/8: y=12/49 2. скорость велосипедиста...
1 - Вычислите среднее арифметическое чисел: а) 5,6; 3,2; 7,1; б) 32,7; 14,8;...
2 - Почему васютка слышал гудок парохода со стороны озера?...
1 - Отметь все слова которые являются словочитанием в предложении белый снег...
2
1. Для начала, мы можем заметить, что треугольник RFT — прямоугольный, так как отрезок FT — высота, опущенная на гипотенузу RF.
2. Зная радиус окружности (12 см), мы можем выразить длину отрезка FR:
FR = 12 см
Также, по условию задачи, FR = RT, поэтому RT также равняется 12 см.
3. Мы можем использовать теорему Пифагора, чтобы найти длину отрезка FT:
FT² = FR² + RT²
FT² = 12² + 12² (подставляем значения FR и RT)
FT² = 144 + 144
FT² = 288
Поэтому, FT = √288
4. Найдем квадратный корень из 288:
FT = √288
FT = √(16 * 18) (разложим 288 на множители)
FT = √16 * √18 (корень из произведения равен произведению корней)
FT = 4√18
FT = 4√(9 * 2) (разложим 18 на множители)
FT = 4 * 3√2 (корень из 9 равен 3)
FT = 12√2
Таким образом, значение FT равно 12√2 см.